
【题目】如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF.那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
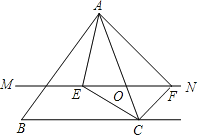
【答案】当点O运动到AC的中点(或OA=OC)时,四边形AECF是矩形.证明见解析.
【解析】
当点O运动到AC的中点(或OA=OC)时,四边形AECF是矩形.由于CE平分∠BCA,那么有∠1=∠2,而MN∥BC,利用平行线的性质有∠1=∠3,等量代换有∠2=∠3,于OE=OC,同理OC=OF,于是OE=OF,而OA=OC,那么可证四边形AECF是平行四边形,又CE、CF分别是∠BCA及其外角的角平分线,易证∠ECF是90°,从而可证四边形AECF是矩形.
当点O运动到AC的中点(或OA=OC)时,四边形AECF是矩形.
证明:如图,

∵CE平分∠BCA,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO,
又∵OA=OC,
∴四边形AECF是平行四边形,
∵CF是∠BCA的外角平分线,
∴∠4=∠5,
又∵∠1=∠2,
∴∠1+∠5=∠2+∠4,
又∵∠1+∠5+∠2+∠4=180°,
∴∠2+∠4=90°,
∴平行四边形AECF是矩形.


科目:初中数学 来源: 题型:
【题目】综合与探究
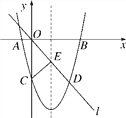
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
(1)求抛物线的解析式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使△FOE≌△FCE.若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店今年1月份的销售额是2万元,3月份的销售额是3.38万元.
(1)求从1月份到3月份,该商店销售额平均每月的增长率;
(2)如果该商店4月份销售额增长率保持不变,销售额能否达到4.5万元,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个质点在第一象限及![]() 轴、
轴、![]() 轴上运动, 在第一秒钟,它从原点运动到
轴上运动, 在第一秒钟,它从原点运动到![]() ,然后接着按图中箭头所示方向运动,且每秒移动一个单位,那么第
,然后接着按图中箭头所示方向运动,且每秒移动一个单位,那么第![]() 秒时质点所在位置的坐标是( )
秒时质点所在位置的坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.
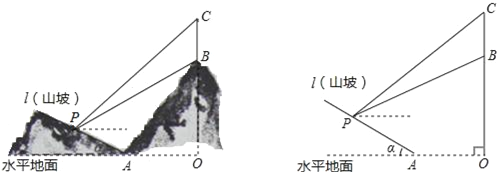
求:
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿![]() 轴做如下移动,第一次点A向左移动3个单位长度到达点
轴做如下移动,第一次点A向左移动3个单位长度到达点![]() ,第二次将点
,第二次将点![]() 向右移动6个单位长度到达点
向右移动6个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动9个单位长度到达点
向左移动9个单位长度到达点![]() ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第![]() 次移动到点
次移动到点![]() ,如果点
,如果点![]() 与原点的距离不小于20,那么
与原点的距离不小于20,那么![]() 的最小值是 .
的最小值是 .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com