
科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表:

科学家经过猜想、推测出l与t之间是二次函数关系.由此可以推测最适合这种植物生长的温度为_______℃.
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为 cm.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,已知AB是⊙O的直径,AB=8,点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,连结OD,过点B作OD的平行线交⊙O于点E、交射线CD于点F.
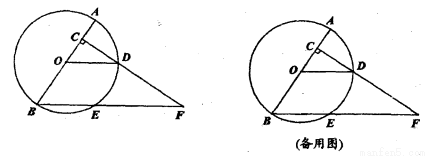
(1)若ED=BE,求∠F的度数:
(2)设线段OC=a,求线段BE和EF的长(用含a的代数式表示);
(3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:解答题
解下列方程:
(1)x2-4x-3=0
(2)(x-2)2=3(x-2)
(3)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,半圆O的直径AB=10,弦AC=6,AD平分∠BAC,则AD的长为( )
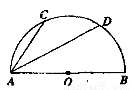
A.2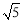 B.3
B.3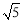 C.4
C.4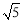 D.20
D.20
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
一组数据:0,2,3,4,4,5的众数和中位数分别是( )
A.3和4 B.4和3 C.3.5和4 D.4和3.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省郑州市九年级第一次质量预测数学试卷(解析版) 题型:解答题
(11分)已知抛物线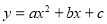
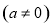 与
与 轴交于A、B两点,与
轴交于A、B两点,与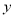 轴交于点C,其中点B在
轴交于点C,其中点B在 轴的正半轴上,点C在
轴的正半轴上,点C在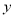 轴的正半轴上,OB=2,OC=8,抛物线的对称轴是直线
轴的正半轴上,OB=2,OC=8,抛物线的对称轴是直线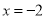 .
.
(1)求此抛物线的表达式;
(2)连接AC、BC、,若点E是线段AB上的一个动点(与点A、点B不重合),过点E做EF//AC交与点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(3)在(2)的基础上说明S是否存在最大值,若存在,请求出S的最大值,并求出此点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com