
 如图所示,∠B=∠D=90°,BC=CD,∠1=30°,则∠2=60°.
如图所示,∠B=∠D=90°,BC=CD,∠1=30°,则∠2=60°.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 为了审核书稿中的错别字,选择抽样调查 | |
| B. | 斜坡的坡度指的是坡角的度数 | |
| C. | 所有的等腰直角三角形都相似 | |
| D. | “经过有交通信号灯的路口,遇到红灯”是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
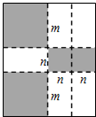 如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为mcm的大正方形,两块是边长都为ncm的小正方形,五块是长宽分别是mcm、ncm的全等小矩形,且m>n.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为mcm的大正方形,两块是边长都为ncm的小正方形,五块是长宽分别是mcm、ncm的全等小矩形,且m>n.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 课间,顽皮的小刚拿着老师的等腰直角三角板放在黑板上画好了的平面直角坐标系内(如图),已知直角顶点H的坐标为(0,1),另一个顶点G的坐标为(4,4),则点K的坐标为(3,-3).
课间,顽皮的小刚拿着老师的等腰直角三角板放在黑板上画好了的平面直角坐标系内(如图),已知直角顶点H的坐标为(0,1),另一个顶点G的坐标为(4,4),则点K的坐标为(3,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
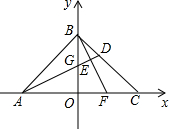 如图,在平面直角坐标系中,OA=OB=OC=6,点G的线段OB上的一个动点,连接AG并延长BC于点D.
如图,在平面直角坐标系中,OA=OB=OC=6,点G的线段OB上的一个动点,连接AG并延长BC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com