
 如图,抛物线y=(x+m)2+m,与直线y=-x相交于E,C两点(点E在点C的左边),抛物线与x轴交于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=-x相交于点D.
如图,抛物线y=(x+m)2+m,与直线y=-x相交于E,C两点(点E在点C的左边),抛物线与x轴交于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=-x相交于点D.分析 (1)由抛物线y=(x+m)2+m与y轴的交点坐标为(0,2),可得m2+m=2,又由抛物线与x轴有两个交点,即可得(x+m)2+m=0有两个不相等的实数根,继而求得答案;
(2)首先作直径CM交弦AB于点G,连接HB,由抛物线y=(x+m)2+m,与直线y=-x相交于E,C两点(点E在点C的左边),可得(x+m)2+m=-x,继而可证得点C是抛物线的顶点,由抛物线与圆的对称性得:CM垂直平分AB,可证得CM⊥直线y=1,然后设A,B两点的横坐标分别为x1,x2,则x1,x2是(x+m)2+m=x2+2mx+m2+m=0的两根,可得x1+x2=-2m,x1•x2=m2+m,再设⊙H的半径为r,CG=-m,HG=-m-r,易证得点H到直线y=1的距离为:-m-r+1=2r-r=r,即可得⊙H与直线y=1相切;
(3)首先连接MD,由⊙H与直线y=1相切于点M,可得△CMN是等腰直角三角形,CM为直径,易得DN=DC,则可求得EC的长,继而求得答案.
解答 (1)解:∵抛物线y=(x+m)2+m与y轴的交点坐标为(0,2),
∴当x=0时,y=m2+m=2,
解得:m1=-2,m2=1;
∵抛物线与x轴有两个交点,
∴(x+m)2+m=0有两个不相等的实数根,
∴m<0,
∴m=-2;
(2)证明:作直径CM交弦AB于点G,连接HB,
∵抛物线y=(x+m)2+m,与直线y=-x相交于E,C两点(点E在点C的左边),
∴(x+m)2+m=-x,
∴(x+m)(x+m+1)=0,
解得:x1=-m,x2=-m-1,
∴点E(-m-1,m+1),C(-m,m);
∴点C是抛物线的顶点,
由抛物线与圆的对称性得:CM垂直平分AB,
∴CM⊥直线y=1,
设A,B两点的横坐标分别为x1,x2,则x1,x2是(x+m)2+m=x2+2mx+m2+m=0的两根,
∴x1+x2=-2m,x1•x2=m2+m,
∴AB=x2-x1=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=2$\sqrt{-m}$,
设⊙H的半径为r,CG=-m,HG=-m-r,
在Rt△HGB中,HG=-m-r,HB=r,GB=$\sqrt{-m}$,
∴(-m-r)2+($\sqrt{-m}$)2=r2,
解得:r=$\frac{1-m}{2}$,
∵HG=-m-r,
∴点H到直线y=1的距离为:-m-r+1=2r-r=r,
∴⊙H与直线y=1相切;
(3)连接MD,
∵⊙H与直线y=1相切于点M,
∴△CMN是等腰直角三角形,
∵CM为直径,
∴∠CDM=90°,
∴DN=DC,
∵点E(-m-1,m+1),C(-m,m),
∴EC=$\sqrt{2}$,
∵DE=2EC,
∴CD=3EC=3$\sqrt{2}$,
∴CN=2CD=6$\sqrt{2}$,
∴CM=2r=6,
∴r=3.
点评 此题属于二次函数的综合题,考查了待定系数法求函数的解析式、圆周角定理、切线的判定与性质以及等腰三角形的性质.此题综合性很强,能准确作出辅助线,并能利用方程思想求解是关键.


科目:初中数学 来源: 题型:选择题
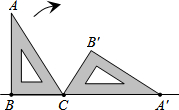 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )| A. | 10πcm | B. | 10$\sqrt{3}$πcm | C. | 15πcm | D. | 20πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC中,AB>AC,∠BAC的平分线与BC的垂直平分线DE交于点D,过点D作DF⊥AB,垂足为F.
已知△ABC中,AB>AC,∠BAC的平分线与BC的垂直平分线DE交于点D,过点D作DF⊥AB,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是等边三角形,D、E分别在BC、AB上,且AE=BD,连接AD、CE交于P,过点C作CH⊥AD于H.
如图,△ABC是等边三角形,D、E分别在BC、AB上,且AE=BD,连接AD、CE交于P,过点C作CH⊥AD于H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将△ABC绕点A顺时针方向旋转α角度到△ADE的位置,设BC与DE交于M点,连接AM.求证:
如图,将△ABC绕点A顺时针方向旋转α角度到△ADE的位置,设BC与DE交于M点,连接AM.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,∠C=∠B=90°,M是BC的中点,DM平分∠ADC.
已知:如图,∠C=∠B=90°,M是BC的中点,DM平分∠ADC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,点E是正方形ABCD的边CD上的一点,点F是BC边延长线上的一点,且有BE=DF,BE的延长线交DF于点G.
如图所示,点E是正方形ABCD的边CD上的一点,点F是BC边延长线上的一点,且有BE=DF,BE的延长线交DF于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com