
【题目】如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.
(Ⅰ)求∠OBC+∠ODC的值;
(Ⅱ)如图1:若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF:
(Ⅲ)如图2:若BF、DG分别平分∠OBC、∠ODC的外角,判断BF与DG的位置关系,并说明理由.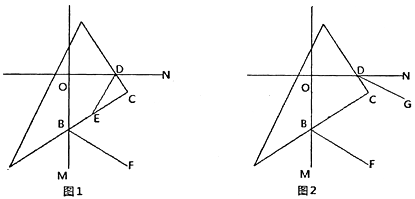
【答案】(Ⅰ)解:∵OM⊥ON,
∴∠MON=90°,
在四边形OBCD中,∠C=∠BOD=90°,
∴∠OBC+∠ODC=360°﹣90°﹣90°=180°;
故答案为180°;
(Ⅱ)证明:延长DE交BF于H,如图1,
∵∠OBC+∠ODC=180°,
而∠OBC+∠CBM=180°,
∴∠ODC=∠CBM,
∵DE平分∠ODC,BF平分∠CBM,
∴∠CDE=∠FBE,
而∠DEC=∠BEH,
∴∠BHE=∠C=90°,
∴DE⊥BF;
(Ⅲ)解:DG∥BF.理由如下:
作CQ∥BF,如图2,
∵∠OBC+∠ODC=180°,
∴∠CBM+∠NDC=180°,
∵BF、DG分别平分∠OBC、∠ODC的外角,
∴∠GDC+∠FBC=90°,
∵CQ∥BF,
∴∠FBC=∠BCQ,
而∠BCQ+∠DCQ=90°,
∴∠DCQ=∠GDC,
∴CQ∥GD,
∴BF∥DG.
【解析】(Ⅰ)先利用垂直定义得到∠MON=90°,然后利用四边形内角和求解;
(Ⅱ)延长DE交BF于H,如图,由于∠OBC+∠ODC=180°,∠OBC+∠CBM=180°,根据等角的补角相等得到∠ODC=∠CBM,由于DE平分∠ODC,BF平分∠CBM,则∠CDE=∠FBE,然后根据三角形内角和可得∠BHE=∠C=90°,于是DE⊥BF;
(Ⅲ)作CQ∥BF,如图2,由于∠OBC+∠ODC=180°,则∠CBM+∠NDC=180°,再利用BF、DG分别平分∠OBC、∠ODC的外角,则∠GDC+∠FBC=90°,根据平行线的性质,由CQ∥BF得∠FBC=∠BCQ,加上∠BCQ+∠DCQ=90°,则∠DCQ=∠GDC,于是可判断CQ∥GD,所以BF∥DG.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补),还要掌握三角形的外角(三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“367人中有2人同月同日生”为必然事件
B.可能性是1%的事件在一次试验中一定不会发生
C.数据3,5,4,1,﹣2的中位数是4
D.检别某批次灯泡的使用寿命,适宜用普查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,薪黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6名,7名,8名,10名,12名这五种情形,并将统计结果绘制成了如图所示的两份不完整的统计图:
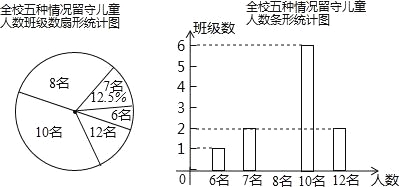
请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补充条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的![]() 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支.
(1)求第一次每支铅笔的进价是多少元?
(2)若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家发改委发布信息,到2019年12月底,高速公路电子不停车快速收费(ETC)用户数量将突破1.8亿,将180 000 000科学记数法表示为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com