
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,以
,以![]() 为一边向外做平行四边形
为一边向外做平行四边形![]() ,连接
,连接![]() ,
,![]() 井延长
井延长![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,且
,且![]() .
.
(1)如图1,若![]() ,求
,求![]() ;
;

(2)如图1,求证:![]() ;
;
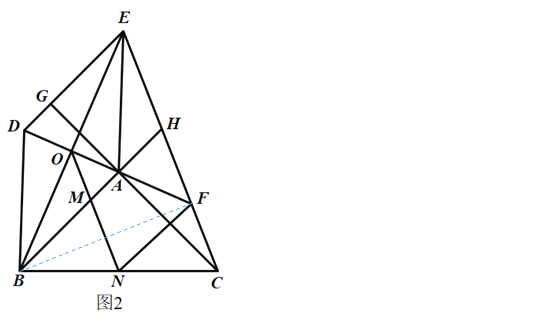
(3)如图2,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,若
,若![]() ,平行四边形
,平行四边形![]() 面积为96,
面积为96,![]() .求
.求![]() 的长.
的长.

【答案】(1)45°;(2)见详解;(3)FN+AN=5![]() +
+![]()
【解析】
(1)首先证明四边形ABDE是菱形,然后利用菱形的性质求出∠EDB的度数,进而求出∠DAG,∠ECB的度数最后利用三角形外角的性质即可求解;
(2)连接BF,由菱形的性质推出△EAF≌△BAF(SAS),根据全等三角形的性质推出∠EFA=∠BFA=45°,进而∠CFB=90°,推出BF2+CF2=BC2,BC2=AB2+AC2=2AB2=2DE2,从而得出BF2+CF2=2DE2
(3)首先通过菱形的面积公式求出BE的长度,进面可求出英形的边长,然后利用三角形中位线的可得出OM,MN.CH的长度,进而利用勾股定理即可求出AH的长度,然后由(2)可知∠BFC=90°,根据中线的性质求得FN=![]() BC=5
BC=5![]() ,则答案可解.
,则答案可解.
解:(1)∵![]() ,
,![]() ,
,
∴AB=BD,
∴平行四边形ABDE是菱形,
∴AB=BD=DE=EA=AC,
∵DE∥AB,∠BAC=90°
∴∠DGA=90°
∵∠EDA=70°
∴∠DAG=180°-∠EDA-∠DGA=180°-70°-90°=20°=∠CAF
∵DE=EA,
∴∠EDA=∠EAD=70°
∴∠GAE=∠EAD-∠CAF=70°-20°=50°
∵EA=AC,
∴∠AEC=∠ACE
∵∠GAE=∠AEC+∠ACE=2∠ACE=50°
∴∠ACE=25°
∴∠EFD=∠ACE +∠CAF=25°+20°=45°
故答案为:∠EFD=45°

(2)证明:如图1,连接BF,
∵平行四边形ABDE是菱形,
∴AE=AB,∴∠EAD=∠BAD=70°
∴∠EAF=∠BAF
在△EAF和△BAF中

∴△EAF≌△BAF(SAS)
∴EF=BF,∠EFA=∠BFA=45°,
∴∠EFB=90°,
∴∠CFB=90°,
∴BF2+CF2=BC2,BC2=AB2+AC2=2AB2=2DE2
∴BF2+CF2=2DE2
(3)如图2,连接BF
∵S菱形ABDE=![]() AD·BE=96,AD=12
AD·BE=96,AD=12
∴BE=16,
∴OE=![]() BE=8,OD=
BE=8,OD=![]() AD=6
AD=6
∴DE=![]()
∴BC=![]()
∵Rt△OEF是等腰直角三角形,
∴EF=2OE,
由(2)结论得,CF=2OD
∴EF=8![]() ,CF=6
,CF=6![]()
∴EF=14![]()
∵O为BE的中点,ON∥EC
∴ON=![]() EC=7
EC=7![]()
∵![]()
∴MN=ON-OM=![]()
∴CH=![]()
∵∠BAC=90°,
∴∠HAC=90°
∴AH=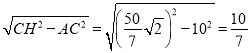
由(2)可知:∠BFC=90°,N是BC的中点,
∴FN=![]() BC=5
BC=5![]() ,
,
∴FN+AN=5![]() +
+![]()
故答案为:FN+AN=5![]() +
+![]()


科目:初中数学 来源: 题型:
【题目】甲、乙两名运动员同时从A地出发到B地,在直线公路上进行骑自行车训练.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米;④甲、乙两名运动员相距5千米时,t=0.5或t=2或t=5.其中正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB=![]() AC时,判断四边形EGCF是什么形状?请说明理由.
AC时,判断四边形EGCF是什么形状?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+ ![]() )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+ ![]() 的自变量x的取值范围是x>0,下表是y与x的几组对应值.
的自变量x的取值范围是x>0,下表是y与x的几组对应值.

① 写出m的值;
②画出该函数图象,结合图象,得出当x=________时,y有最小值,y最小=________;
提示:在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.试用配方法求函数y=x+ ![]() (x>0)的最小值,解决问题(2).
(x>0)的最小值,解决问题(2).
(2)【解决问题】
直接写出“问题情境”中问题的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点A1,B1,C1分别是BC、AC、AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.
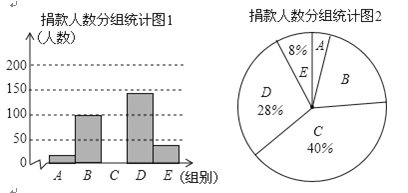
被调查的捐款人数分组统计表:
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com