

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 “构造法”是一种重要方法,它没有固定的模式.要想用好它,需要有敏锐的观察、丰富的想象、灵活的构思.应用构造法解题的关键有二:一是要有明确的方向,即为什么目的而构造;二是要弄清条件的本质特点,以便重新进行组合.
“构造法”是一种重要方法,它没有固定的模式.要想用好它,需要有敏锐的观察、丰富的想象、灵活的构思.应用构造法解题的关键有二:一是要有明确的方向,即为什么目的而构造;二是要弄清条件的本质特点,以便重新进行组合.| 5 |
| 10 |
| 13 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 5a |
| 2a |
| 17a |
查看答案和解析>>
科目:初中数学 来源:2013年浙江省湖州市高级中等学校招生考试数学 题型:013
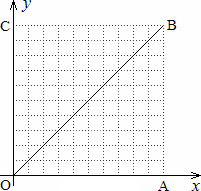
下图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为![]() ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
A.16
B.15
C.14
D.13
查看答案和解析>>
科目:初中数学 来源:2008年北京市石景山区初三数学一模试卷及答案 题型:022
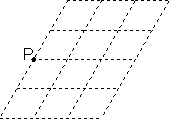
如下图,在由12个边长都为1且有一个锐角为60°的小菱形组成的网格中,点P是其中的一个顶点,以点P为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长________.
查看答案和解析>>
科目:初中数学 来源:2008年北京市石景山区初三一模数学试卷 题型:022
如下图,在由12个边长都为1且有一个锐角为60°的小菱形组成的网格中,点P是其中的一个顶点,以点P为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com