��1���жϣ�EN��MF��ȣ���EN=MF������F��ֱ��NE�� ������������ 3��
��˵�������һ����2�֣�
��2������������������������������������������������������������������������ 4��
֤����
��һ������DE��DF�� ������������������������������������������������������������������������������������������������������������������������������������������������������ 5��
�ߡ�ABC�ǵȱ������Σ���AB=AC=BC��
�֡�D��E��F�����ߵ��е㣬
��DE��DF��EFΪ�����ε���λ�ߣ���DE=DF=EF����FDE=60�㣮
�֡�MDF+��FDN=60�㣬��NDE+��FDN=60�㣬
���MDF=��NDE�� ���������������������������������������������������������������������������������������������������������������������������������������������������������������� 7��
�ڡ�DMF�͡�DNE�У�DF=DE��DM=DN����MDF=��NDE��
���DMF�ա�DNE�� �������������������������������������������������������������������������������������������������������������������������������������������������������������� 8��
��MF=NE�� ���������������������������������������������������������������������������������������������������������������������������������������������������������������� 9��

������
�ӳ�EN����EN����F�� �������������������������������������������������������������������������������������������������������������������������������������������� 5��
�ߡ�ABC�ǵȱ������Σ���AB=AC=BC���֡�D��E��F�����ߵ��е㣬��EF=DF=BF��
�ߡ�BDM+��MDF=60�㣬��FDN+��MDF=60�㣬���BDM=��FDN������������������������������������������������ 7��
�֡�DM=DN����ABM=��DFN=60�㣬���DBM�ա�DFN�������������������������������������������������������������������� 8��
��BM=FN����BF=EF�� ��MF=EN�������������������������������������������������������������������������������������������������������������������������� 9��
������
����DF��NF�� ���������������������������������������������������������������������������������������������������������������������������������������������������������������������������� 5��
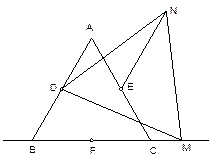
�ߡ�ABC�ǵȱ������Σ���AC=BC=AC��
�֡�D��E��F�����ߵ��е㣬��DFΪ�����ε���λ�ߣ���DF=

AC=

AB=DB��
�֡�BDM+��MDF=60�㣬��NDF+��MDF=60�㣬���BDM=��FDN�� ������������7��
�ڡ�DBM�͡�DFN�У�DF=DB��
DM=DN����BDM=��NDF�����DBM�ա�DFN��
���B=��DFN=60�㣮��������������������������������������������������8��
�֡ߡ�DEF�ǡ�ABC�����е������ɵ������Σ�
���DFE=60�㣮��ɵõ�N��EF�ϣ���MF=EN��������������������������9��
��3������ͼ�Σ������߶�NE���� ������������������������������������������������������������������������������������������������������������������������������ 10��
MF��EN��ȼ���F��ֱ��NE�ϵĽ�����Ȼ��������MF=NE�������� �������������������������������� 11��

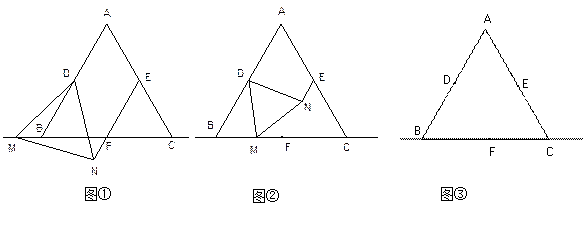

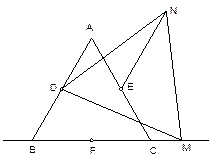
 AC=
AC= AB=DB��
AB=DB��

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�

 ,�Խ���AC��BD�ཻ�ڵ�0����ֱ��AC�Ƶ�0˳ʱ����ת���ֱ�BC��AD�ڵ�E��F.
,�Խ���AC��BD�ཻ�ڵ�0����ֱ��AC�Ƶ�0˳ʱ����ת���ֱ�BC��AD�ڵ�E��F.

 ƽ����
ƽ���� ����
���� ��ֵΪ��������
��ֵΪ��������


 �Գƣ����B=_________
�Գƣ����B=_________