
 由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,两棵树的株距(两棵树的水平距离)为3米.在点A有一只蚂蚁想尽快爬到位于B、C两点之间的D处,且CD=0.1米,问它怎样走最近?为什么?
由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,两棵树的株距(两棵树的水平距离)为3米.在点A有一只蚂蚁想尽快爬到位于B、C两点之间的D处,且CD=0.1米,问它怎样走最近?为什么?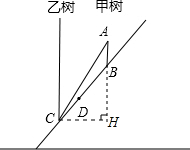 答:蚂蚁沿着A-B-D路线走最近.理由如下:
答:蚂蚁沿着A-B-D路线走最近.理由如下: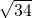 +0.1,AB+BD=1+4.9=5.9,
+0.1,AB+BD=1+4.9=5.9,

科目:初中数学 来源: 题型:
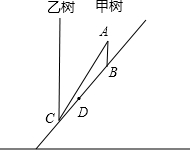 由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,两棵树的株距(两棵树的水平距离)为3米.在点A有一只蚂蚁想尽快爬到位于B、C两点之间的D处,且CD=0.1米,问它怎样走最近?为什么?
由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,两棵树的株距(两棵树的水平距离)为3米.在点A有一只蚂蚁想尽快爬到位于B、C两点之间的D处,且CD=0.1米,问它怎样走最近?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
 由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图,其树恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,已知两棵树的水平距离为3米,请计算出这棵树原来的高度(结果保留根号)
由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图,其树恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,已知两棵树的水平距离为3米,请计算出这棵树原来的高度(结果保留根号)查看答案和解析>>
科目:初中数学 来源:江苏期中题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2013年山东省滨州市滨城区中考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com