
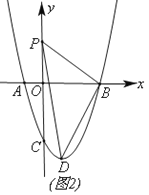
【题目】如图,在平面直角坐标中,抛物线y=ax2-2ax-3a(a≠0)与x轴交于A、B(A在B的左侧),与y轴交于点C,且OC=3OA.
(1)如图(1)求抛物线的解析式;
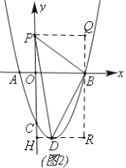
(2)如图(2)动点P从点O出发,沿y轴正方向以每秒1个单位的速度移动,点D是抛物线顶点,连接PB、PD、BD,设点P运动时间为t(单位:秒),△PBD的面积为S,求S与t的函数关系式;
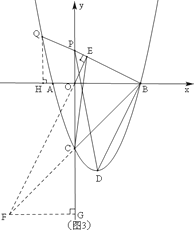
(3)如图(3)在(2)的条件下,延长BP交抛物线于点Q,过点O作OE⊥BQ,垂足为E,连接CE、CB,若CE=CB,求t值,并求出此时的Q点坐标.


【答案】(1)y=x2-2x-3;(2)S=t+6;(3)t=![]() ;Q (
;Q (![]() ,
, ![]() ).
).
【解析】试题分析:(1)令y=0,求出A、B的坐标,再由OC=3OA,得到a的值,即可得到结论;
(2)过B点作QR∥y轴,作PQ⊥DR,垂足为Q,过D点作DH∥x轴,交y轴于点H,交BR于点R.S△PDB=S矩形PQRH-(S△PQB+S△PDH+S△DBR),代入相关数据即可得到结论;
(3)延长EO、BC相交于点F,过F作作FG⊥y轴,垂足为G,ON⊥AD,过Q作QH⊥x轴,垂足为H.可证明△FCG≌△BCO,得到CG=CO=3,FG=BO=3.在△GOF中,可得到tan∠FOG=![]() .由∠OBE=∠FOG,得到tan∠OBE=
.由∠OBE=∠FOG,得到tan∠OBE=![]() ,从而可求的t的值.
,从而可求的t的值.
设点Q(m.m2-2m-3),则QH=m2-2m-3,BH=3-m,得到tan∠OBE=![]() ,BH=2QH,3-m=2(m2-2m-3),即可得到m的值,进而得到Q 的坐标.
,BH=2QH,3-m=2(m2-2m-3),即可得到m的值,进而得到Q 的坐标.
试题解析:解:(1)令y=0,ax2-2ax-3a=0,a(x-3)(x+1)=0.∵a≠0,∴ ![]() ,
, ![]() .∵A在B的左侧,∴A(-1,0),B(3,0).∵OC=3OA=3,∴C(0,-3),∴-3a=-3,∴a=1,
.∵A在B的左侧,∴A(-1,0),B(3,0).∵OC=3OA=3,∴C(0,-3),∴-3a=-3,∴a=1,
∴抛物线为:y=x2-2x-3.
(2)如图(2)过B点作QR∥y轴,作PQ⊥DR,垂足为Q,过D点作DH∥x轴,交y轴于点H,交BR于点R.
∵D是抛物线定点,∴D(1,-4).∵P(0,
∴PQ=3,BQ=t,BR=4,DR=2,DH=1,PH=t+4,∴S△PDB=S矩形PQRH-(S△PQB+S△PDH+S△DBR)
∴S=PH×PQ-![]() (PQ×BQ+PH×DH+DR ×BR) =(t+4)×3-
(PQ×BQ+PH×DH+DR ×BR) =(t+4)×3-![]() ([3×t+(t+4)×1+2×4]
([3×t+(t+4)×1+2×4]
∴ S=t+6.
(3)如图(3),延长EO、BC相交于点F,过F作作FG⊥y轴,垂足为G,ON⊥AD,
过Q作QH⊥x轴,垂足为H.
∵OE⊥BQ,∴∠BEF=900.∵CE=CB,∴∠BEC=∠EBC.
∵∠BEC+∠CEF=900,∠EBC+∠BFE=900,∴∠CEF=∠BFE,∴CF=CE=CB.∵FG⊥y轴,∠FGC=∠BOC=900,∠FCG=∠BCO,∴△FCG≌△BCO,∴CG=CO=3,FG=BO=3.
在△GOF中,∠FGC=900,FG=3,OG=6,∴tan∠FOG=![]() .
.
∵∠BOE+∠OBE=900.,∠BOEC+∠POE=900,∴∠OBE=∠POE,∠POE=∠FOG,∴∠OBE=∠FOG,∴tan∠OBE=![]() ,∴OP=
,∴OP= ![]() =
=![]() ,∴t=
,∴t=![]() .
.
设点Q(m.m2-2m-3),则QH=m2-2m-3,BH=3-m,∴tan∠OBE=![]() ,BH=2QH,3-m=2(m2-2m-3),∴m1=
,BH=2QH,3-m=2(m2-2m-3),∴m1=![]() ,m2=3(舍去),∴m=
,m2=3(舍去),∴m=![]() ,∴Q (
,∴Q (![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为鼓励返乡农民工创业,宿州市政府制定了小型企业的优惠政策,许多小型企业应运而生.某镇统计了该镇今年1~5月新注册小型企业的数量,并将结果绘制成如下两种不完整的统计图:
今年1~5月各月新注册小型企业今年1~5月各月新注册小型企业数量占今年前数量折线统计图五月新注册小型企业总量的百分比扇形统计图
(1)某镇今年1~5月新注册小型企业一共有 家,请将折线统计图补充完整.
(2)该镇今年3月新注册的小型企业中,只有2家是餐饮企业.现从3月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一个角的补角比它的余角的 3 倍大 30°,求这个角的度数;
(2)如图,点 C、D在线段 AB上, D是线段 AB的中点, AC ![]() AD , AB6,求线段 CD的长.
AD , AB6,求线段 CD的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块Rt△ABC的纸片,∠ABC=900,AB=6,BC=8,将△ABC沿AD折叠,使点B落在AC上的E处,则BD的长为( )
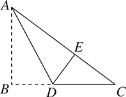
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
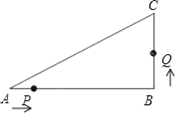
【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P开始从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm,点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.
(1)出发2秒后,求PQ的长;
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,则求出几秒后第一次形成等腰三角形;若不能,则说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读第①小题的计算方法,再计算第②小题.
①–5![]() +(–9
+(–9![]() )+17
)+17![]() +(–3
+(–3![]() )
)
解:原式=[(–5)+(–![]() )]+[(–9)+(–
)]+[(–9)+(–![]() )]+(17+
)]+(17+![]() )+[(–3+(–
)+[(–3+(–![]() )]
)]
=[(–5)+(–9)+(–3)+17]+[(–![]() )+(–
)+(–![]() )+(–
)+(–![]() )+
)+![]() ]
]
=0+(–1![]() )
)
=–1![]() .
.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000![]() )+(﹣1999
)+(﹣1999![]() )+4000
)+4000![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
在数轴上,点 A 在原点 0 的左边,距离原点 4 个单位长度,点 B 在原点的右边,点 A 和点 B 之间的距离为 14个单位长度.
(1)点 A 表示的数是 ,点 B 表示的数是 ;
(2)点 A、B 同时出发沿数轴向左移动,速度分别为 1 个单位长度/秒,3 个单位长度/秒,经过多少秒,点 A 与点 B重合?
(3)点 M、N 分别从点 A、B 出发沿数轴向右移动,速度分别为 1 个单位长度/秒、2 个单位长度/秒,点 P 为 ON 的中点,设 OP-AM 的值为 y,在移动过程中,y 值是否发生变化?若不变,求出 y 值;若变化,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com