如图，在△ABC中，D为AB边上一点、F为AC的中点，过点C作CE//AB交DF的延长线于点E，连结AE．
（1）求证：四边形ADCE为平行四边形．
（2）若EF=2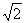
，
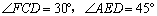，求DC的长．
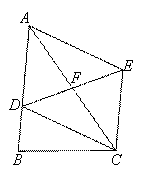
（1）证明：∵CE//AB，∴∠DAF=∠ECF．
∵F为AC的中点，∴AF=CF．
在△DAF和△ECF中
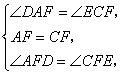
∴ △DAF≌△ECF．
∴ AD=CE．
∵CE//AB，
∴ 四边形ADCE为平行四边形． （2）作FH⊥DC于点H．
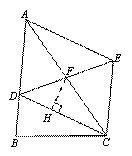∵ 四边形ADCE为平行四边形．
∴ AE//DC，DF= EF=2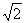， ∴∠FDC =∠AED=45°．
在Rt△DFH中，∠DHF=90°，DF=2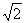，∠FDC=45°，
∴ sin∠FDC=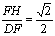
，得FH=2，
tan∠FDC=
，得DH=2．
在Rt△CFH中，∠FHC=90°，FH=2，∠FCD=30°，∴ FC=4．
由勾股定理，得HC=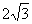
．
∴ DC=DH+HC=2+．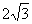
科目：初中数学 来源： 题型：
观察下面的式子：（12分）
S1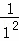=1+
+
，S2=1++
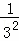，S3=1+
+
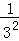…Sn=1+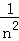
+
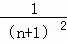
（1）计算：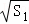
= ，
= ；猜想
= （用n的代数式表示）；
（2）计算：S=+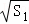
++…+
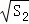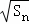（用n的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
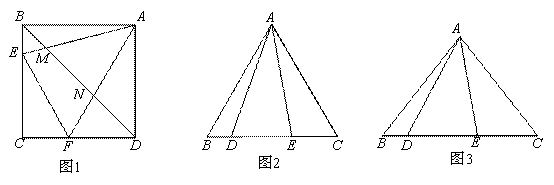
（1）如图1，点E、F分别是正方形ABCD的边BC、CD上的点，∠EAF=45°，连接EF，
则EF、BE、FD之间的数量关系是：EF=BE+FD．连结BD，交AE、AF于点M、N，且MN、BM、DN满足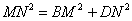
，请证明这个等量关系；
（2）在△ABC中， AB=AC，点D、E分别为BC边上的两点．
①如图2，当∠BAC=60°，∠DAE=30°时，BD、DE、EC应满足的等量关系是__________________；
②如图3，当∠BAC=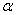
，(0°<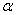<90°)，∠DAE=
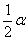时，BD、DE、EC应满足的等量关系是____________________．【参考：
】
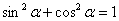查看答案和解析>>
科目：初中数学 来源： 题型：
已知抛物线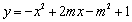
与x轴交点为A、B（点B在点A的右侧），与y轴交于点C．
（1）试用含m的代数式表示A、B两点的坐标；
（2）当点B在原点的右侧，点C在原点的下方时，若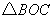
是等腰三角形，求抛物线的解析式；
（3）已知一次函数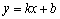
，点P（n，0）是x轴上一个动点，在（2）的条件下，过点P作垂直于x轴的直线交这个一次函数的图象于点M，交抛物线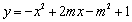于点N，若只有当
时，点M位于点N的下方，求这个一次函数的解析式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
.
B C D
，则
的度数是
的整数解