
”¾ĢāÄæ”æ°“Ķ¼ĢīæÕ£¬²¢×¢Ć÷ĄķÓÉ£®
¢ÅĶź³ÉÕżČ·µÄÖ¤Ć÷£ŗČēĶ¼£¬ŅŃÖŖAB”ĪCD£¬ĒóÖ¤£ŗ”ĻBED=”ĻB+”ĻD
Ö¤Ć÷£ŗ¹żEµć×÷EF”ĪAB£Ø¾¹żÖ±ĻßĶāŅ»µćÓŠĒŅÖ»ÓŠŅ»ĢõÖ±ĻßÓėÕāĢõÖ±ĻßĘ½ŠŠ£©
”ą”Ļ1= £Ø £©
”ßAB”ĪCD£ØŅŃÖŖ£©
”ąEF”ĪCD£ØČē¹ūĮ½ĢõÖ±ĻßÓėĶ¬Ņ»Ö±ĻßĘ½ŠŠ£¬ÄĒĆ“ĖüĆĒŅ²Ę½ŠŠ£©
”ą”Ļ2= £Ø £©
ÓÖ”ĻBED=”Ļ1+”Ļ2
”ą”ĻBED=”ĻB+”ĻD £ØµČĮæ“ś»»£©£®
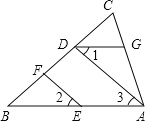
¢ĘČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬EF”ĪAD£¬”Ļ1=”Ļ2£¬”ĻBAC=70”ć£®½«Ēó”ĻAGDµÄ¹ż³ĢĢīŠ“ĶźÕū£®
½ā£ŗŅņĪŖEF”ĪAD£ØŅŃÖŖ£©
ĖłŅŌ”Ļ2=”Ļ3£®£Ø £©
ÓÖŅņĪŖ”Ļ1=”Ļ2£¬ĖłŅŌ”Ļ1=”Ļ3£®£ØµČĮæ“ś»»£©
ĖłŅŌAB”Ī £Ø £©
ĖłŅŌ”ĻBAC+ =180”ć£Ø £©£®
ÓÖŅņĪŖ”ĻBAC=70”ć£¬ĖłŅŌ”ĻAGD=110”ć£®

Ķ¼¢Å Ķ¼¢Ę
”¾“š°ø”æ(1) ”ĻB £ØĮ½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£©
”ĻD £ØĮ½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£©
(2) £ØĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬Ī»½ĒĻąµČ£©£»
DG £ØÄŚ“ķ½ĒĻąµČ£¬Į½Ö±ĻßĘ½ŠŠ£©£®
”ĻAGD £ØĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½Ē»„²¹£©
”¾½āĪö”æ·ÖĪö£ŗ£Ø1£©øł¾ŻĘ½ŠŠĻߵĊŌÖŹ½ā¾öĪŹĢā£»£Ø2£©øł¾ŻĘ½ŠŠĻßµÄÅŠ¶ØÓėŠŌÖŹĒó½ā£®
±¾Ģā½āĪö£ŗ
Ö¤Ć÷£ŗ¹żEµć×÷EF”ĪAB£Ø¾¹żÖ±ĻßĶāŅ»µćÓŠĒŅÖ»ÓŠŅ»ĢõÖ±ĻßÓėÕāĢõÖ±ĻßĘ½ŠŠ£©
”ą”Ļ1= ”ĻB £ØĮ½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£©
”ßAB”ĪCD£ØŅŃÖŖ£©
”ąEF”ĪCD£ØČē¹ūĮ½ĢõÖ±ĻßÓėĶ¬Ņ»Ö±ĻßĘ½ŠŠ£¬ÄĒĆ“ĖüĆĒŅ²Ę½ŠŠ£©
”ą”Ļ2= ”ĻD £ØĮ½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£©
ÓÖ”ĻBED=”Ļ1+”Ļ2
”ą”ĻBED=”ĻB+”ĻD £ØµČĮæ“ś»»£©£®
¢ĘČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬EF”ĪAD£¬”Ļ1=”Ļ2£¬”ĻBAC=70”ć£®½«Ēó”ĻAGDµÄ¹ż³ĢĢīŠ“ĶźÕū£®
½ā£ŗŅņĪŖEF”ĪAD£ØŅŃÖŖ£©
ĖłŅŌ”Ļ2=”Ļ3£®£ØĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬Ī»½ĒĻąµČ£©
ÓÖŅņĪŖ”Ļ1=”Ļ2£¬ĖłŅŌ”Ļ1=”Ļ3£®£ØµČĮæ“ś»»£©
ĖłŅŌAB”Ī DG £ØÄŚ“ķ½ĒĻąµČ£¬Į½Ö±ĻßĘ½ŠŠ£©
ĖłŅŌ”ĻBAC+ ”ĻAGD =180”ć£ØĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½Ē»„²¹£©£®
ÓÖŅņĪŖ”ĻBAC=70”ć£¬ĖłŅŌ”ĻAGD=110”ć£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČō2m-4Óė3m-1ŹĒĶ¬Ņ»øöŹżµÄĘ½·½øł£¬ŌņmµÄÖµŹĒ£Ø £©
A. -3B. 1C. -3»ņ1D. 3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠĘßĆūĶ¬Ń§Õ¾³ÉŅ»ÅÅÕÕ±ĻŅµ¼ĶÄīÕÕ£¬ĘäÖŠ¼×±ŲŠėÕ¾ŌŚÕżÖŠ¼ä£¬²¢ĒŅŅŅ”¢±ūĮ½Ī»Ķ¬Ń§ŅŖÕ¾ŌŚŅ»Ęš£¬Ōņ²»Ķ¬µÄÕ¾·ØÓŠ£Ø £©
A.240ÖÖ
B.192ÖÖ
C.96ÖÖ
D.48ÖÖ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Čż½ĒŠĪÖ½Ę¬ÖŠ£¬AB=8cm£¬BC=6cm£¬AC=5cm£®ŃŲ¹żµćBµÄÖ±ĻßÕŪµžÕāøöČż½ĒŠĪ£¬Ź¹µćCĀäŌŚAB±ßÉĻµÄµćE“¦£¬ÕŪŗŪĪŖBD£¬Ēó”÷ADEµÄÖܳ¤£® 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖa£¬bĪŖŹµŹż£¬£Øa2+b2£©2©£Øa2+b2£©©6=0£¬Ōņ“śŹżŹ½a2+b2µÄÖµĪŖ£Ø””””£©
A.2
B.3
C.©2
D.3»ņ©2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
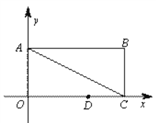
”¾ĢāÄæ”æČēĶ¼,ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ,¾ŲŠĪOABCµÄ±ßOAŌŚyÖįµÄÕż°ėÖįÉĻ,OCŌŚxÖįµÄÕż°ėÖįÉĻ£¬OA=1,OC=2,µćDŌŚ±ßOCÉĻĒŅOD=1.25£®
£Ø1£©ĒóÖ±ĻßACµÄ½āĪöŹ½£®
£Ø2£©ŌŚyÖįÉĻŹĒ·ń“ęŌŚµćP,Ö±ĻßPDÓė¾ŲŠĪ¶Ō½ĒĻßAC½»ÓŚµćM,Ź¹µĆ”÷DMCĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ,Ö±½ÓŠ“³öĖłÓŠ·ūŗĻĢõ¼žµÄµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø3£©Å×ĪļĻßy=-x2¾¹żŌõŃłĘ½ŅĘ,²ÅÄÜŹ¹µĆĘ½ŅĘŗóµÄÅ×ĪļĻß¹żµćDŗĶµćE£ØµćEŌŚyÖįÕż°ėÖįÉĻ£©,ĒŅ”÷ODEŃŲDEÕŪµžŗóµćOĀäŌŚ±ßABÉĻO/“¦£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĢģ£¬Ņ»Źß²Ė¾ÓŖ»§ÓĆ234ŌŖĒ®“ÓŹß²ĖÅś·¢ŹŠ³”ÅśĮĖĪ÷ŗģŹĮŗĶĒŃ×Ó¹²50¹«½ļµ½²ĖŹŠ³”Č„Āō£¬Ī÷ŗģŹĮŗĶĒŃ×ÓÕāĢģµÄÅś·¢¼ŪÓėĮćŹŪ¼ŪČēĻĀ±ķĖłŹ¾£ŗ

ĪŹ£ŗ£Ø1£©øĆ¾ÓŖ»§µ±ĢģŌŚŹß²ĖÅś·¢ŹŠ³”ÅśĮĖĪ÷ŗģŹĮŗĶĒŃ×Óø÷¶ąÉŁ¹«½ļ£æ
£Ø2£©Ėūµ±ĢģĀōĶźÕāŠ©Ī÷ŗģŹĮŗĶĒŃ×ÓÄÜ׬¶ąÉŁĒ®£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涞“ĪŗÆŹży£½(x©2)2+1µÄĶ¼ĻóµÄ¶Ō³ĘÖįĪŖ_____£®¶„µć×ų±źŹĒ_____£®ÓėyÖį½»µć×ų±źŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=15£¬BC=14£¬AC=13£¬Ēó”÷ABCµÄĆ껿£® Ä³Ń§Ļ°Š”×é¾¹żŗĻ×÷½»Į÷£¬øų³öĮĖĻĀĆęµÄ½āĢāĖ¼Ā·£¬ĒėÄć°“ÕÕĖūĆĒµÄ½āĢāĖ¼Ā·£¬Ķź³É½ā“š¹ż³Ģ£®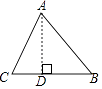
£Ø1£©×÷AD”ĶBCÓŚD£¬ÉčBD=x£¬ÓĆŗ¬xµÄ“śŹżŹ½±ķŹ¾CD£¬ŌņCD=£»
£Ø2£©Ēėøł¾Ż¹“¹É¶ØĄķ£¬ĄūÓĆAD×÷ĪŖ”°ĒÅĮŗ”±½ØĮ¢·½³Ģ£¬²¢Ēó³öxµÄÖµ£»
£Ø3£©ĄūÓĆ¹“¹É¶ØĄķĒó³öADµÄ³¤£¬ŌŁ¼ĘĖćČż½ĒŠĪµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com