
【题目】不等式组  的整数解的个数为( )
的整数解的个数为( )
A.6
B.7
C.8
D.9
【答案】D
【解析】解:  ,
,
解①得x<3,
解②得x≥﹣6.
则不等式组的解集是:﹣6≤x<3.
则整数解是﹣6,﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2.共有9个.
所以答案是:D.
【考点精析】解答此题的关键在于理解一元一次不等式组的解法的相关知识,掌握解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ),以及对一元一次不等式组的整数解的理解,了解使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解).


科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.




(1)如图1,若![]() ,点
,点![]() 在
在![]() 外部,则有
外部,则有![]() ,又可证
,又可证![]() ,得
,得![]() ,将点
,将点![]() 移到
移到![]() 内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则
内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则![]() 之间有何数量关系?请证明你的结论;
之间有何数量关系?请证明你的结论;
(2)在如图2中,将直线![]() 绕点
绕点![]() 逆时针方向旋转一定角度交直线
逆时针方向旋转一定角度交直线![]() 于点
于点![]() 如图3,则
如图3,则![]()
![]() 之间有何数量关系? (不需证明);
之间有何数量关系? (不需证明);
(3)根据(2)的结论,求如图4中![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,直线![]() 与直线
与直线![]() 交与点
交与点![]() .
.
![]() 轴上是否存在点P,使
轴上是否存在点P,使![]() 的面积是
的面积是![]() 面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
![]() 如图2,若点E是x轴上的一个动点,点E的横坐标为
如图2,若点E是x轴上的一个动点,点E的横坐标为![]() ,过点E作直线
,过点E作直线![]() 轴于点E,交直线
轴于点E,交直线![]() 于点F,交直线
于点F,交直线![]() 于点G,求m为何值时,
于点G,求m为何值时,![]() ≌
≌![]() ?请说明理由.
?请说明理由.
![]() 在
在![]() 的前提条件下,直线l上是否存在点Q,使
的前提条件下,直线l上是否存在点Q,使![]() 的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
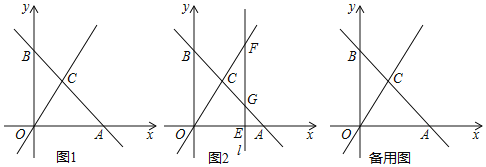
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据表中的信息判断,下列语句中正确的是

( )
A.![]() =1.59
=1.59
B.235的算术平方根比15.3小
C.只有3个正整数n满足![]()
D.根据表中数据的变化趋势,可以推断出16.12将比256增大3.19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() .
.

(1)如图 1,若![]() ,求
,求![]() 的度数;
的度数;
(2)把“![]() °”改为“
°”改为“![]() ”,射线
”,射线![]() 沿射线
沿射线![]() 平移,得到
平移,得到![]() ,其它条件不变(如 图 2 所示),探究
,其它条件不变(如 图 2 所示),探究![]() 的数量关系;
的数量关系;
(3)在(2)的条件下,作![]() ,垂足为
,垂足为![]() ,与
,与![]() 的角平分线
的角平分线![]() 交于点
交于点![]() ,若
,若![]() , 用含 α 的式子表示
, 用含 α 的式子表示![]() (直接写出答案).
(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1 所示,△ ABC 和△ AEF 为等边三角形,点 E 在△ ABC 内部,且 E 到点 A、B、C 的距离分别为 3、4、5,求∠AEB 的度数.
(2)如图 2,在△ ABC 中,∠CAB=90°,AB=AC,M、N 为 BC 上的两点,且∠MAN=45°,MN2 与 NC2+BM2 有何关系?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx+c经过A(﹣1,0),C(2,﹣3)两点,与y轴交于点D,与x轴交于另一点B.
x2+bx+c经过A(﹣1,0),C(2,﹣3)两点,与y轴交于点D,与x轴交于另一点B.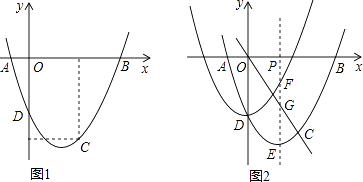
(1)求此抛物线的解析式及顶点坐标;
(2)若将此抛物线平移,使其顶点为点D,需如何平移?写出平移后抛物线的解析式;
(3)过点P(m,0)作x轴的垂线(1≤m≤2),分别交平移前后的抛物线于点E,F,交直线OC于点G,求证:PF=EG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你根据如图所示的阿宝与仙鹤的对话,解答下列问题:
(1)仙鹤为什么说多边形内角和的度数不可能是![]() ;
;
(2)若图中仙鹤所提到的外角的度数为![]() ,请分别求仙鹤所画的多边形的内角和的度数与边数.
,请分别求仙鹤所画的多边形的内角和的度数与边数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com