
【题目】已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△AˊBD.
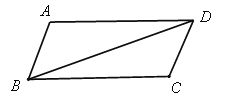
(1)利用尺规作出△AˊBD.(要求保留作图痕迹,不写作法);
(2)设D Aˊ 与BC交于点E,求证:△BAˊE≌△DCE.
科目:初中数学 来源: 题型:
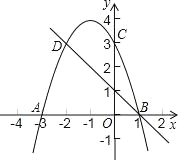
【题目】如图,二次函数y1=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y2=mx+n的图象经过B、D两点.
(1)求二次函数的解析式及点D的坐标;
(2)根据图象写出y2>y1时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③△ABC≌△APC;④PA∥BC;⑤∠APH=∠BPC,其中正确结论的个数是( )
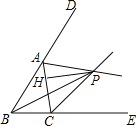
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
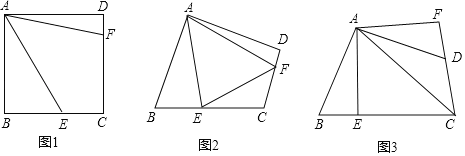
【题目】(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD.
(2)如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
(3)如图3,四边形ABCD中,∠BAD≠90°,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD交CD延长线于F,若BC=8,CD=3,则CE= .(不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b在数轴上的对应点位置如图所示 ![]()
(1)用“<”连接0、﹣a、﹣b、﹣1
(2)化简:|a|﹣2|a+b﹣1|﹣ ![]() |b﹣a﹣1|
|b﹣a﹣1|
(3)若a2c+c<0,且c+b>0,求 ![]() +
+ ![]() ﹣
﹣ ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于矩形的说法中正确的是( )
A.对角线相等的四边形是矩形
B.矩形的对角线相等且互相平分
C.对角线互相平分的四边形是矩形
D.矩形的对角线互相垂直且平分
查看答案和解析>>
科目:初中数学 来源: 题型:
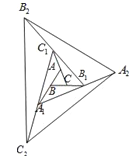
【题目】如图,△ABC的面积为1,分别倍长(延长一倍)AB,BC,CA得到△A1B1C1,再分别倍长A1B1,B1C1,C1A1得到△A2B2C2.…按此规律,倍长n次后得到的△A2017B2017C2017的面积为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com