
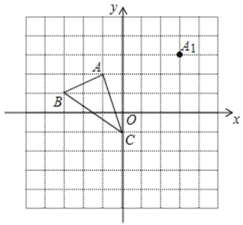
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,﹣1).
(1)写出A、B两点的坐标
(2)经过平移,△ABC的顶点A移到了点A1,画出平移后的△A1B1C1;若△ABC内有一点P(a,b),直接写出按(2)的平移变换后得到对应点P1的坐标.
(3)画出△ABC绕点C旋转180°后得到的△A2B2C2.
科目:初中数学 来源: 题型:
【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.
(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有4个小球,分别标有1,2,3,7四个数字,这些小球除所标数字不同外,其余方面完全相同,甲、乙两人每次同时从袋子中各随机摸出一个小球,记下小球上的数字,并计算它们的和.
(1)请用画树状图或列表的方法,求两数和是8的概率;
(2)甲、乙两人想用这种方法做游戏,他们规定:若两数之和是2的倍数时,甲得3分;若两数之和是3的倍数时,乙得2分;当两数之和是其他数值时,两人均不得分.你认为这个游戏公平吗?请说明理由;若你认为不公平,请你修改得分规则,使游戏公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”![]() 是近时期网络流行语,像一个人脸郁闷的神情
是近时期网络流行语,像一个人脸郁闷的神情![]() 如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案
如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案![]() 阴影部分
阴影部分![]() 设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
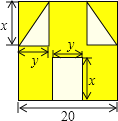
(1)用含有x、y的代数式表示下图中“囧”的面积;
(2)当![]() ,
,![]() 时,求此时“囧”的面积.
时,求此时“囧”的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象交于A(-3,2),B(n,4)两点.
)的图象交于A(-3,2),B(n,4)两点.
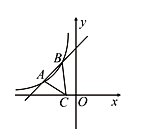
(1)求一次函数与反比例函数的解析式;
(2)点C(-1,0)是![]() 轴上一点,求△ABC的面积.
轴上一点,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水质量的需求越来越高,我市某公司根据市场需求准备销售A、B两种型号的净水器,每台A型净水器比每台B型净水器进价多300元,用48000元购进A型净水器与用36000元购进B型净水器的数量相等.
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A、B两种型号的净水器共400台进行销售,其中A型的台数不超过B型的台数,A型净水器每台售价1500元,B型净水器每台售价1100元,怎样安排进货才能使售完这400台净水器所获利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
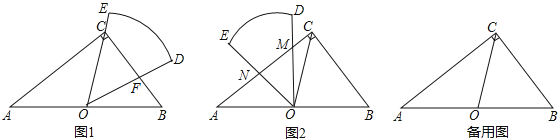
【题目】如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.
(1)证明△COF是等腰三角形,并求出CF的长;
(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
.在数学综合与实践课上,老师以“出行方式的选择"为主题,请同学们发现和提出问题并分断和解决问题
问题情境
随着互联网的普及和城市交通的多样化,人们出行的时间与方式有了更多的选择.某市有出租车.滴滴快车和神州专车三种网约车,收费标准见下图(该市规定网约车行驶的平均速度为![]() 公里时)
公里时)

问题一
“奋进小组”提出的问题是:如果乘坐这三种网约车的里程数都是10公里.他们发现乘坐出租车最节省钱.费用为_______元;
问题二
“质疑小组”提出了两个问题,请从![]() 两个问题中任选一问做答,
两个问题中任选一问做答,
A.从甲地到乙地,乘坐出租车比滴滴快车节省![]() 元,求甲.乙两地间的里程数.
元,求甲.乙两地间的里程数.
B.神州专车和滴滴快车对第一次下单的乘客有如下优惠活动:神州专车收费打八折,另外加![]() 元的空车费;滴滴快车超过
元的空车费;滴滴快车超过![]() 公里收费立减
公里收费立减![]() 元.如果两位顾客都是第一次下单,分别乘坐神州专车、滴滴快车且收费相同,求这两位顾客乘车的里程数.
元.如果两位顾客都是第一次下单,分别乘坐神州专车、滴滴快车且收费相同,求这两位顾客乘车的里程数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com