某班参加一次智力竞赛,共a,b,c三题,每题或者得满分或者得0分.其中题a满分20分,题b、题c满分分别为25分.竞赛结果,每个学生至少答对了一题,三题全答对的有1人,答对其中两道题的有15人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为25,答对题b的人数与答对题c的人数之和为20,问这个班的平均成绩是多少分?
【答案】
分析:假设x
a、x
b、x
c分别表示答对题a、题b、题c的人数.根据:答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为25,答对题b的人数与答对题c的人数之和为20,列出三元一次方程组,求出方程组的解.再根据:竞赛结果,每个学生至少答对了一题,三题全答对的有1人,答对其中两道题的有15人,求得答对1题的人数,进而求出该班总人数.再根据每题分数,求得平均成绩.
解答:解:设x
a、x
b、x
c分别表示答对题a、题b、题c的人数.
则有
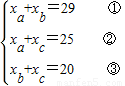
,
由①+②+③得x
a+x
b+x
c=37 ④
由④-①得x
c=8
同理可得x
a=17,x
b=12
∴答对一题的人数为37-1×3-2×15=4,全班人数为1+4+15=20
∴平均成绩为
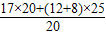
=42.
答:这个班的平均成绩是42分.
点评:本题解决以求分别表示答对题a、题b、题c的人数做为突破口,进而求出全班人数,求得平均成绩.

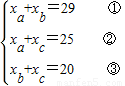 ,
,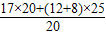 =42.
=42.
