
【题目】如图,在![]() 中,
中,![]() 是高线,
是高线,![]() 、
、![]() 是角平分线,它们相交于点
是角平分线,它们相交于点![]() ,
,![]() ,
,![]() ,求
,求![]() 与
与![]() 的度数.
的度数.
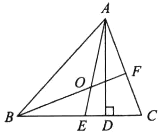
【答案】∠EAD=5°,∠BOA=125°
【解析】
因为AD是高,所以∠ADC=90°,又因为∠C=70°,求出∠DAC度数,根据∠EAD=∠EAC-∠DAC可求∠EAD;因为∠BAC=50°,∠C=70°,所以∠BAO=25°,∠ABC=60°,BF是∠ABC的角平分线,则∠ABO=30°,故∠BOA的度数可求.
∵AD⊥BC
∴∠ADC=90°
∵∠C=70°
∴∠DAC=180°-90°-70°=20°,
∵AE平分∠BAC,
∴∠CAE=![]() ×50°=25°
×50°=25°
∴∠EAD=∠EAC-∠DAC=25°-20°=5°;
∵∠BAC=50°,∠C=70°
∴∠BAO=25°,∠ABC=60°
∵BF是∠ABC的角平分线
∴∠ABO=30°
∴∠BOA=180°-∠BAO-∠ABO=180°-25°-30°=125°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
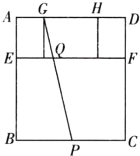
【题目】如图,一个长方形窗框![]() 被
被![]() 分成上下两个长方形,上部分长方形又被分成三个小长方形,其中
分成上下两个长方形,上部分长方形又被分成三个小长方形,其中![]() ,
,![]() 为
为![]() 的四等分点(
的四等分点(![]() 在
在![]() 左侧)且
左侧)且![]() .一晾衣杆斜靠在窗框上的
.一晾衣杆斜靠在窗框上的![]() 位置,
位置,![]() 为
为![]() 中点.若
中点.若![]() ,
,![]() 分长方形
分长方形![]() 的左右面积之比为
的左右面积之比为![]() ,则
,则![]() 分长方形
分长方形![]() 的左右面积之比为________.(用含
的左右面积之比为________.(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() ,若平移点
,若平移点![]() 到点
到点![]() ,使以点
,使以点![]() 为顶点的四边形是菱形,则正确的平移方法是( )
为顶点的四边形是菱形,则正确的平移方法是( )

A. 向左平移(![]() )个单位,再向上平移1个单位
)个单位,再向上平移1个单位
B. 向左平移![]() 个单位,再向下平移1个单位
个单位,再向下平移1个单位
C. 向右平移![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
D. 向右平移2个单位,再向上平移1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
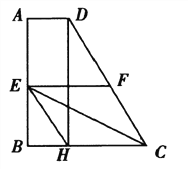
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:![]() 为等边三角形,点E为射线AC上一点,点D为射线CB上一点,
为等边三角形,点E为射线AC上一点,点D为射线CB上一点,![]() .
.
(1)如图1,当E在AC的延长线上且![]() 时,AD是
时,AD是![]() 的中线吗?请说明理由;
的中线吗?请说明理由;
(2)如图2,当E在AC的延长线上时,![]() 等于AE吗?请说明理由;
等于AE吗?请说明理由;
(3)如图3,当D在线段CB的延长线上,E在线段AC上时,请直接写出AB、BD、AE的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在真角坐标系中,矩形0ABC的顶点A,C在坐标轴上,点B(4,2);过点D(0,3)和E(6,0)的直线分别与AB、BC交于点M、N.
(1)求直线DE的函数表达式和点M,N的坐标;
(2)若函数y=![]() (k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(3)求△OMN的面积S;
(4)若函教y=![]() (k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.
(k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年日本奥运会的比赛门票开始接受公众预订.下表为日本奥运会官方票务网站公布的几种球类比赛的门票价格,某球迷准备用8000元预订10张下表中比赛项目的门票.
比赛项目 | 票价(元/场) |
男篮 | 1000 |
足球 | 800 |
乒乓球 | 500 |
(1)若全部资金用来预订男篮门票和乒乓球门票,问他可以订男篮门票和乒乓球门票各多少张?
(2)若在现有资金8000元允许的范围内和总票数不变的前提下,他想预订下表中三种球类门票,其中男篮门票数与足球门票数相同,且乒乓球门票的费用不超过男篮门票的费用,求他能预订三种球类门票各多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
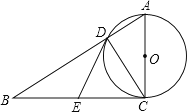
(1)求证:点E是边BC的中点;
(2)求证:BC2=BDBA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com