练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．菱形ABCD的周长是20，对角线AC、BD相交于点O，若BD=6，则菱形ABCD的面积是24．

    分析 根据菱形的周长可以计算菱形的边长，菱形的对角线互相垂直平分，已知AB，AO根据勾股定理即可求得BO的值，根据对角线长即可计算菱形ABCD的面积．

    解答 解：菱形周长为20，则AB=5，
    菱形对角线互相垂直平分，
    ∴AO=3，
    ∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=4，
    ∴BD=2BO=8，
    故菱形ABCD的面积为$\frac{1}{2}$×6×8=24．
    故答案为24．

    点评 本题考查了菱形对角线互相垂直平分的性质，注意菱形各边长相等的性质，勾股定理在直角三角形中的运用，本题中根据勾股定理求BO的值是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届广东省梅州市九年级下学期第一次月考数学试卷（解析版） 题型：单选题

    下列事件是必然事件的是（　　）

    A. 任意购买一张电影票，座位号是奇数 B. 打开电视，正在播出“奔跑吧，兄弟”

    C. 13名同学中至少有两名同学出生的月份相同 D. 抛掷一枚硬币，反面朝上

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．求下列各数的平方根
    （1）100；
    （2）$\frac{49}{25}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．顺次连接一个四边形的各边中点，得到一个矩形，则下列四边形中：①平行四边形；②菱形；③矩形；④对角线互相垂直的四边形．满足条件的四边形是②④（把你认为正确的序号填在横线上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．若$\sqrt{x-2}$+$\root{3}{4-x}$有意义，则x的取值范围是（　　）
    A．x≥2B．2≤x≤4C．x＜4D．2＜x＜4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

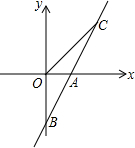    8．如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，-2）．
    （1）求直线AB的解析式；
    （2）若直线AB上的点C在第一象限，且S△BOC=2.5，求点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点，以C（0，1）为圆心，1为半径的圆上找一动点P，连接PA、PB，则△PAB面积的最大值是（　　）
    A．10B．9C．6+$\frac{5\sqrt{2}}{2}$D．9$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，O是菱形ABCD一条对角线BD上的一个点，它是菱形一边AB的距离（OE）是2cm，那么O到BC的距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．若m＞n，下列不等式不一定成立的是（　　）
    A．m2＞n2B．m+2＞n+2C．$\frac{m}{2}$＞$\frac{n}{2}$D．-2m＜-2n

    查看答案和解析>>

    同步练习册答案