
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得点P在射线BC上,且∠APB=![]() ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.

(1)当⊙O的半径为1时
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D,E,F中,⊙O的依附点是 ;
②点T在直线y=﹣![]() x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣2x+2与x轴、y轴分别交于点M、N,若线段MN上的所有点都是⊙C的依附点,请求出圆心C的横坐标n的取值范围.
【答案】(1)①E、F;②![]() <t<
<t<![]() 或﹣
或﹣![]() <t<﹣
<t<﹣![]() ;(2)2<n<
;(2)2<n<![]() 或﹣2<n<1﹣
或﹣2<n<1﹣![]() .
.
【解析】
(1)①根据P为⊙C的依附点,由圆内角度的相互转换,判断出当r<OP<3r(r为⊙C的半径)时,P为⊙C的依附点,由此即可判断;
②分两种情形:点T在第二象限或第四象限分别求解即可;
(2)分两种情形:点C在点M的右侧,点C在点M的左侧,根据题意分析计算即可.
解:(1)①当⊙O的半径为1时,即圆心C与原点重合,
如图,设B、D为圆O与x轴的左右交点,A为圆上任意一点,

∵OA=OD,
∴∠OAD=∠ODA,
∴∠ADB=![]() ∠AOB,
∠AOB,
∵∠APB=![]() ∠AOB,
∠AOB,
∴∠ADB=![]() ∠APB,
∠APB,
∴∠DAP=∠APB,
∴AD=DP,
当点A和点B重合时,OP=3r,
当点A与点D重合时,OP=r,
∵0°<∠ACB<180°,即0°<∠AOB<180°
∴r<OP<3r
根据P为⊙C的依附点,可知:当r<OP<3r(r为⊙C的半径)时,点P为⊙C的依附点.
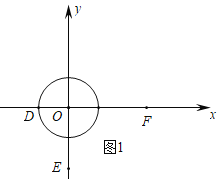
如图1中,∵D(1,0),E(0,2),F(2.5,0),
∴OD=1,OE=2,OF=2.5,
∴1<OE<3,1<OF<3,
∴点E,F是⊙C的依附点,
故答案为:E、F;
②如图2,
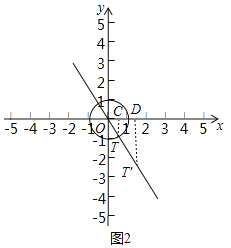
∵点T在直线y=![]() 上,
上,
∴点T在第二象限或第四象限,直线y=![]() 与x轴所夹的锐角为60°,
与x轴所夹的锐角为60°,
当点T在第四象限,当OT=1时,作CT⊥x轴,易求点![]() ,当OT'=3时,作DT'⊥x轴,易求D
,当OT'=3时,作DT'⊥x轴,易求D![]() ,
,
∴满足条件的点T的横坐标t的取值范围![]() ,
,
当点T在第二象限,同理可得满足条件的点T的横坐标t的取值范围![]() ,
,
综上所述:满足条件的点T的横坐标t的取值范围:![]() 或
或![]() ,
,
(2)如图3中,当点C在点M的右侧时,
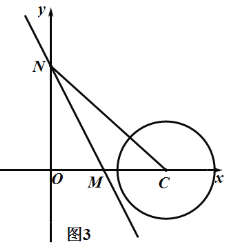
由题意M(1,0),N(0,2),
当CN=3时,OC=![]() ,此时C
,此时C![]() ,
,
当CM=1时,此时C(2,0),
∴满足条件的n的值的范围为![]() ;
;
如图4中,当点C在点M的右侧时,
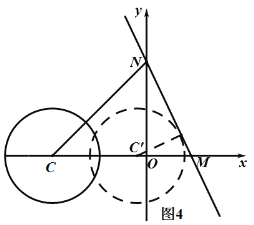
当⊙C与直线MN相切时,
由题意M(1,0),N(0,2),∴MN=![]() ,
,
∴sin∠OMN=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
当CM=3时,C(2,0),此时![]() ,满足题意,
,满足题意,
∴满足条件的m的值的范围为![]() ,
,
综上所述,满足条件的n的值的范围为:![]() 或
或![]() .
.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( )
 A、2
A、2
B、4
C、![]()
D、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作![]() 交AP于E点.
交AP于E点.
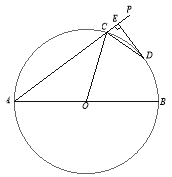
(1)求证:DE为⊙O的切线;
(2)若DE=3,AC=8,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳能是来自太阳的辐射能量,对于地球上的人类来说,太阳能是对环境无任何污染的可再生能源,因此许多国家都在大力发展太阳能.如图是2013﹣2017年我国光伏发电装机容量统计图.根据统计图提供的信息,判断下列说法不合理的是( )
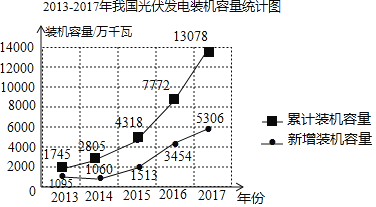
A.截至2017年底,我国光伏发电累计装机容量为13078万千瓦
B.2017年我国光伏发电新装机容量占当年累计装机容量的50%
C.2013﹣2017年,我国光伏发电新增装机容量的平均值约为2500万千瓦
D.2013﹣2017年,我国光伏发电新增装机容量先减少后增加
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,点Q为CA延长线上一点,延长QD交BC于点P,连接OD,∠ADQ=![]() ∠DOQ.
∠DOQ.
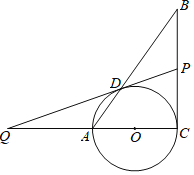
(1)求证:PD是⊙O的切线;
(2)若AQ=AC,AD=4时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长;
(3)点F在抛物线上运动,是否存在点F,使△BFC的面积为6,如果存在,求出点F的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=6,Rt△AB'C'可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,则线段B'C的长为______.
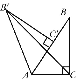
查看答案和解析>>
科目:初中数学 来源: 题型:
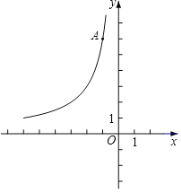
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (x<0)的图象经过点A(﹣1,6).
(x<0)的图象经过点A(﹣1,6).
(1)求k的值;
(2)已知点P(a,﹣2a)(a<0),过点P作平行于x轴的直线,交直线y=﹣2x﹣2于点M,交函数y=![]() (x<0)的图象于点N.
(x<0)的图象于点N.
①当a=﹣1时,求线段PM和PN的长;
②若PN≥2PM,结合函数的图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
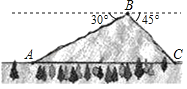
【题目】我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图所示,其中山脚A、C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米,由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°,若在A、C两地间打通一隧道,求隧道最短为多少米(结果取整数,参考数据![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com