
【题目】如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD于点F.

(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠A=90°,∠B=30°,CD=CA,D在BC上,∠ADE=45°,E在AB上,则∠BED的度数是( )
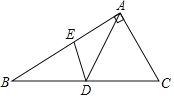
A.60°B.75°C.80°D.85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为正方形ABCD的对角线,点E为DC边上一点(不与C、D重合),连接BE,以E为旋转中心,将线段EB逆时针旋转90°,得到线段EF,连接DF.
(1)请在图中补全图形.
(2)求证:AC∥DF.
(3)探索线段ED、DF、AC的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
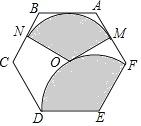
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量休闲凉亭AB的高度,某数学兴趣小组在水平地面D处竖直放置一个标杆CD,并在地面上水平放置一个平面镜E,使得B、E、D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到凉亭顶端A,在F处测得凉亭A顶端的仰角为30°,平面镜E的俯角为45°,FD=2米,求休闲凉亭AB的高度.(结果保留根号)
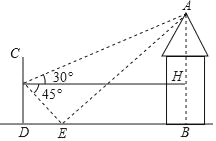
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:

根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,![]() 的三个顶点都在边长为
的三个顶点都在边长为![]() 的小正方形的格点上,关
的小正方形的格点上,关![]() 于
于![]() 轴的对称图形为
轴的对称图形为![]() ,以
,以![]() 与
与![]() 组成一个基本图形,不断复制与平移这个基本图形,得到图形所示的图形
组成一个基本图形,不断复制与平移这个基本图形,得到图形所示的图形
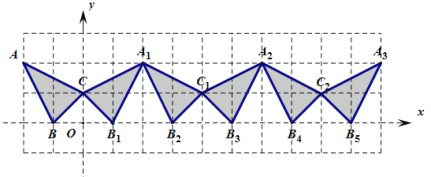
(1)观察以上图形并填写下列各点坐标:
![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 为正整数)
为正整数)
(2)若![]() 是这组图形中的一个三角形,当
是这组图形中的一个三角形,当![]() 时,则
时,则![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com