
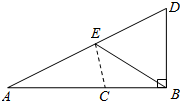
 数学课上,老师按下面的方法作线段AB的黄金分割点C(如图),
数学课上,老师按下面的方法作线段AB的黄金分割点C(如图),分析 (1)根据题意和勾股定理求出AC与BC的长;
(2)根据黄金分割的比值进行判断即可.
解答 解:(1)∵AB=1,
∴BD=$\frac{1}{2}$,
∴AD=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$,
∴AE=$\frac{\sqrt{5}-1}{2}$,即AC=$\frac{\sqrt{5}-1}{2}$,
BC=AB-AC=$\frac{3-\sqrt{5}}{2}$;
(2)∵$\frac{AC}{AB}$=$\frac{\sqrt{5}-1}{2}$,
∴点C是线段AB的黄金分割点.
点评 本题考查的是黄金分割的概念和勾股定理的应用,掌握把一条线段分成两部分,使其中较长的线段作为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
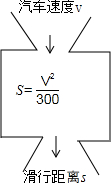 在平整的路面上.某型号汽车紧急刹车后仍将滑行S米,一般地有经验公式S=$\frac{{V}^{2}}{300}$,其中V表示刹车前汽车的速度(单位:千米/时).
在平整的路面上.某型号汽车紧急刹车后仍将滑行S米,一般地有经验公式S=$\frac{{V}^{2}}{300}$,其中V表示刹车前汽车的速度(单位:千米/时).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| +7 | +5 | -4 | +6 | +4 | +3 | -3 | -2 | +8 | +1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com