
分析 (1)①+②+③求出x+y+z=6④,④-①求出z,④-②求出x,④-③求出y;
(2)先求出x,即可得出二元一次方程组,求出方程组的解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+y=3①}\\{y+z=4②}\\{z+x=5③}\end{array}\right.$
①+②+③得:2x+2y+2z=12,
x+y+z=6④,
④-①得:z=3,
④-②得:x=2,
④-③得:y=1,
所以原方程的解为:$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=3}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x+4x=7①}\\{2x+3y+z=9②}\\{5x-9y+7z=8③}\end{array}\right.$
由①得:x=1,
把x=1代入②得:3y+z=7④,
把x=1代入③得:-9y+7z=3⑤,
由④和⑤组成方程组$\left\{\begin{array}{l}{3y+z=7}\\{-9y+7z=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{y=\frac{23}{15}}\\{z=\frac{12}{5}}\end{array}\right.$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=\frac{23}{15}}\\{z=\frac{12}{5}}\end{array}\right.$.
点评 本题考查了解三元一次方程组,能把三元一次方程组转化成二元一次方程组或一元一次方程是解此题的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:填空题
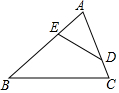 如图,在△ABC中,D,E分别是AC和AB上的点,AD=3cm,AC=4cm,AE=2cm,且$\frac{AD}{AB}$=$\frac{AE}{AC}$,则AB=6cm,BE=4cm.
如图,在△ABC中,D,E分别是AC和AB上的点,AD=3cm,AC=4cm,AE=2cm,且$\frac{AD}{AB}$=$\frac{AE}{AC}$,则AB=6cm,BE=4cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
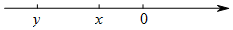 已知x,y两个实数在数轴上位置如图所示,则|y-x|+$\sqrt{{{(x-y)}^2}}$=( )
已知x,y两个实数在数轴上位置如图所示,则|y-x|+$\sqrt{{{(x-y)}^2}}$=( )| A. | 2x | B. | 2y | C. | 2x-2y | D. | 2y-2x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com