
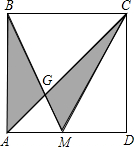
 如图,正方形ABCD的面积为1,M是AD的中点,求图中阴影部分的面积.
如图,正方形ABCD的面积为1,M是AD的中点,求图中阴影部分的面积.| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
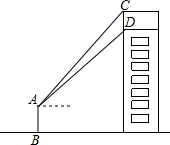 如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈0.606.cos37.3≈0.7955,tan37.3°≈0.7618)
如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈0.606.cos37.3≈0.7955,tan37.3°≈0.7618)查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| BC |
 |
| BD |
| 1 |
| 2 |
 |
| CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com