
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() 为半径的⊙
为半径的⊙![]() 交
交![]() 于点
于点![]() ,
, ![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)判断直线![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
, ![]() ,
, ![]() ,求线段
,求线段![]() 的长.
的长.

【答案】(1)直线DE与⊙O相切,理由见解析;
(2)DE的长为![]() .
.
【解析】(1)直线DE与⊙O相切,理由如下:连接OD,由OD=OA,利用等边对等角得到一对角相等,等量代换得到∠ODE为直角,即可得证;
(2)连接OE,设DE=x,则EB=ED=x,CE=8-x,在Rt△OCE中,利用勾股定理列出关于x的方程,求出方程得到x的值,即可确定出DE的长.
解:(1)直线DE与⊙O相切,理由如下:
连接OD,

∵OD=OA,∴∠A=∠ODA,
∵EF是BD的垂直平分线,
∴EB=ED, ∴∠B=∠EDB,
∵∠C=90°,∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°﹣90°=90°,
∴直线DE与⊙O相切;
(2)连接OE,
设DE=x,则EB=ED=x,CE=8﹣x,
∵∠C=∠ODE=90°,∴OC2+CE2=OE2=OD2+DE2,
∴42+(8﹣x)2=22+x2,
解得: ![]() , 则DE=
, 则DE=![]() .
.
“点睛”本题考查了直线与圆的位置关系,以及线段垂直平分线定理,熟练掌握直线与圆相切的性质是解题的关键.


科目:初中数学 来源: 题型:
【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.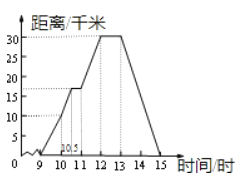
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四个三角形,分别满足下列条件:①一个角等于另外两个内角之和;②三个内角之比为3:4:5;③三边之比为5:12:13;④三边长分别为5,24,25.其中直角三角形有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数![]() 的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.
的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.
(1)求k的值;
(2)在(1)的条件下,若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象从左到右交于Q,R,S三点,且点Q的坐标为(-1,-1),点R(
的图象从左到右交于Q,R,S三点,且点Q的坐标为(-1,-1),点R(![]() ,
, ![]() ),S(
),S(![]() ,
, ![]() )中的纵坐标
)中的纵坐标![]() ,
, ![]() 分别是一元二次方程
分别是一元二次方程![]() 的解,求四边形AQBS的面积
的解,求四边形AQBS的面积![]() ;
;
(3)在(1),(2)的条件下,在x轴下方是否存在二次函数![]() 图象上的点P使得
图象上的点P使得![]() =2
=2![]() ,若存在,求出点P的坐标;若不存在,请说明理由.
,若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com