
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 调查一批新型节能灯泡的使用寿命 | |
| B. | 调查长江流域的水污染情况 | |
| C. | 调查市场上某品牌饮料的质量情况 | |
| D. | 调查奥运会1000米参赛运动员兴奋剂的使用情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
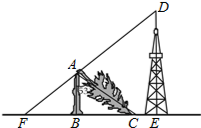 如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成60°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.
如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成60°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
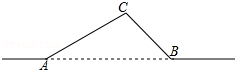 如图,一条光纤线路从A地到B地需要经过C地,图中AC=40千米,
如图,一条光纤线路从A地到B地需要经过C地,图中AC=40千米,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…,则S5的值为128.
在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…,则S5的值为128.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com