
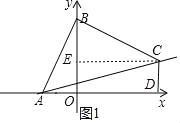
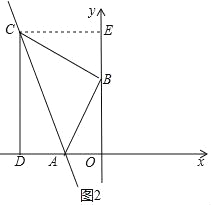
【题目】如图,在平面鱼角坐标系xOy中,A(﹣3,0),点B为y轴正半轴上一点,将线段AB绕点B旋转90°至BC处,过点C作CD垂直x轴于点D,若四边形ABCD的面积为36,则线AC的解析式为_____.

【答案】y=![]() x+1或y=﹣3x﹣9.
x+1或y=﹣3x﹣9.
【解析】
过C作CE⊥OB于E,则四边形CEOD是矩形,得到CE=OD,OE=CD,根据旋转的性质得到AB=BC,∠ABC=90°,根据全等三角形的性质得到BO=CE,BE=OA,求得OA=BE=3,设OD=a,得到CD=OE=|a﹣3|,根据面积公式列方程得到C(﹣6,9)或(6,3),设直线AB的解析式为y=kx+b,把A点和C点的坐标代入即可得到结论.
解:过C作CE⊥OB于E,
则四边形CEOD是矩形,
∴CE=OD,OE=CD,
∵将线段AB绕点B旋转90°至BC处,
∴AB=BC,
∠ABC=90°,
∴∠ABO+∠CBO=∠CBO+∠BCE=90°,
∴∠ABO=∠BCE,
∵∠AOB=∠BEC=90°,
∴△ABO≌△BCO(AAS),
∴BO=CE,BE=OA,
∵A(﹣3,0),
∴OA=BE=3,
设OD=a,
∴CD=OE=|a﹣3|,
∵四边形ABCD的面积为36,
∴![]() AOOB+
AOOB+![]() (CD+OB)OD=
(CD+OB)OD=![]() ×3×a+
×3×a+![]() (a﹣3+a)×a=36,
(a﹣3+a)×a=36,
∴a=±6,
∴C(﹣6,9)或(6,3),
设直线AB的解析式为y=kx+b,
把A点和C点的坐标代入得,![]() 或
或![]()
解得: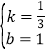 或
或![]() ,
,
∴直线AB的解析式为![]() 或y=﹣3x﹣9.
或y=﹣3x﹣9.
故答案为:![]() 或y=﹣3x﹣9.
或y=﹣3x﹣9.


科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 是常数)经过点
是常数)经过点![]() .
.
(![]() )求该抛物线的解析式和顶点坐标.
)求该抛物线的解析式和顶点坐标.
(![]() )抛物线与
)抛物线与![]() 轴另一交点为点
轴另一交点为点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,平行于
,平行于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() ,
, ![]() ,与直线
,与直线![]() 交于点
交于点![]() .
.
①求直线![]() 的解析式.
的解析式.
②若![]() ,结合函数的图像,求
,结合函数的图像,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探寻“勾股数”:直角三角形三边长是整数时我们称之为“勾股数”,勾股数有多少?勾股数有规律吗?
(1)请你写出两组勾股数.
(2)试构造勾股数.构造勾股数就是要寻找3个正整数,使他们满足“两个数的平方和(或差)等于第三数的平方”,即满足以下形式:
① 2+ 2= 2;或② 2﹣ 2= 2
③要满足以上①、②的形式,不妨从乘法公式入手.我们已经知道③(x+y)2﹣(x﹣y)2=4xy.如果等式③右边也能写成 2的形式,就能符合②的形式.
因此不妨设x=m2,y=n2,(m、n为任意正整数,m>n),请你写出含m、n的这三个勾股数并证明它们是勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() , 纵坐标
, 纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的是 .
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②抛物线与
; ②抛物线与![]() 轴的交点为
轴的交点为![]() ;
;
③抛物线的对称轴是:直线![]() ; ④在对称轴左侧
; ④在对称轴左侧![]() 随
随![]() 增大而增大.
增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图线段AB和CD表示两面镜子,且直线AB∥直线CD,光线EF经过镜子AB反射到镜予CD,最后反射到光线GH.光线反射时,∠1=∠2,∠3=∠4,下列结论:①直线EF平行于直线GH;②∠FGH的角平分线所在的直线垂直于直线AB;③∠BFE的角平分线所在的直线垂直于∠4的角平分线所在的直线;④当CD绕点G顺时针旋转90时,直线EF与直线GH不一定平行,其中正确的是( )

A. ①②③④B. ①②③C. ②③D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB= ![]() ,∠EFA=60°,则四边形A′B′EF的周长是( )
,∠EFA=60°,则四边形A′B′EF的周长是( )

A. 1+3![]() B. 3+
B. 3+![]() C. 4+
C. 4+![]() D. 5+
D. 5+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于![]() AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
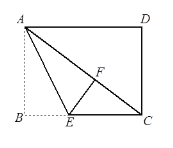
【题目】如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com