【题目】图1，图2，图3是三张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，
两点都在格点上，连结
，请完成下列作图：
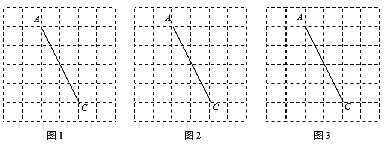
(1)以为对角线在图1中作一个正方形，且正方形各顶点均在格点上.
(2)以为对角线在图2中作一个矩形，使得矩形面积为6，且矩形各顶点均在格点上.
(3)以为对角线在图3中作一个面积最小的平行四边形，且平行四边形各顶点均在格点上.
科目：初中数学 来源： 题型：
【题目】小丽暑假期间参加社会实践活动，从某批发市场以批发价每个m元的价格购进100个手机充电宝，然后每个加价n元到市场出售(结果用含m，n的式子表示)
(1)求售出100个手机充电宝的总售价为多少元?
(2)由于开学临近，小丽在成功售出60个充电宝后，决定将剩余充电宝按售价8折出售，并很快全部售完.(注:售价的8折即按原售价的80%出售)
①她的总销售额是多少元?
②假如不采取降价销售，且也全部售完，她将比实际销售多盈利多少元?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F.
(1)求证：△AEF≌△DEB；
(2)求证：四边形ADCF是菱形；
(3)若AC＝4，AB＝5，求菱形ADCF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
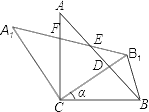
【题目】如图，△ABC中，∠ACB＝90，AC＝BC，将△ABC绕点C逆时针旋转α角（0＜α＜90）得到△A1B1C，连结BB1.设CB1交AB于D，A1B1分别交AB、AC于E、F，
（1）在图中不再添加其它任何线段的情况下，请你找出一对全等的三角形，并加以证明（△ABC与△A1B1C全等除外）；
（2）当△BB1D是等腰三角形时，求α.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明早晨跑步，他从自己家出发，向东跑了2km到达小彬家，继续向东跑了1.5km到达小红家，然后又向西跑了4.5km到达学校，最后又向东，跑回到自己家．
（1）以小明家为原点，以向东为正方向，用1个单位长度表示1km，在图中的数轴上，分别用点A表示出小彬家，用点B表示出小红家，用点C表示出学校的位置；
（2）求小彬家与学校之间的距离；
（3）如果小明跑步的速度是250m/min，那么小明跑步一共用了多长时间？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE＝
∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．
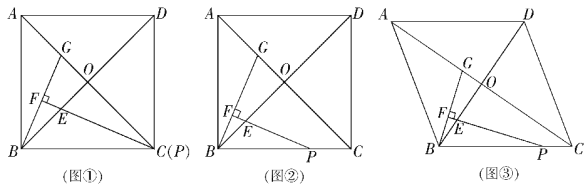
（1） 当点P与点C重合时（如图①）．求证：△BOG≌△POE；（4分）
（2）通过观察、测量、猜想：
= ，并结合图②证明你的猜想；（5分）
（3）把正方形ABCD改为菱形，其他条件不变（如图③），若∠ACB=α，求的值．（用含α的式子表示）（5分）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．若AE=1，则FM的长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．
（1）求证：CD是⊙O的切线；
（2）过点B作⊙O的切线交CD的延长线于点E，BC=6， 
．求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在平面直角坐标系xOy中（如图），已知抛物线y=﹣x2+bx+c经过点A（2，2），对称轴是直线x=1，顶点为B．
（1）求这条抛物线的表达式和点B的坐标；
（2）点M在对称轴上，且位于顶点上方，设它的纵坐标为m，联结AM，用含m的代数式表示∠AMB的余切值；
（3）将该抛物线向上或向下平移，使得新抛物线的顶点C在x轴上．原抛物线上一点P平移后的对应点为点Q，如果OP=OQ，求点Q的坐标．
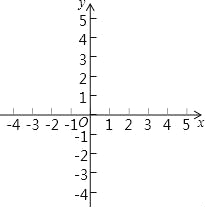
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
