
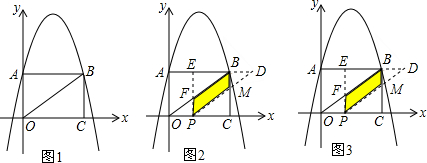
���� ��1�����㣨0��3���ͣ�5��-2�����뼴�����b��c��ֵ�������ý⣬���ɵ�A���B�Գƿ��������B��������Ϊ3�������ý⣻
��2������ƽ�Ƶ����ʣ��Լ���ֱ�������������ж��ı���EPCB�Ǿ��Σ���BEF�ա�PCM�����������ú���t��ʽ�ӱ�ʾ���ı���BFPM������������䷽�����Եý⣻
��3����OE=OC��EC=OC��OE=EC����������н�𣬼��ɵõ�����Ĵ𰸣�
��� �⣺��1�����㣨0��3���ͣ�5��-2������y=-x2+bx+c�ã�$\left\{\begin{array}{l}{c=-3}\\{-25+5b+c=-2}\end{array}\right.$��
��ã�b=4��c=3��
��y=-x2+4x+3��
�ߵ�B���A���ڶԳ���Գƣ�
��3=-x2+4x+3��
��ã�x=0��x=4��
��B��4��3����
��2����ƽ�Ƶ����ʿ�֪��BO��BD��OA��PE��
��OA��x�ᣬBC��x�ᣬ��EP��x�ᣬ
��AB��OC�����EPC=��BCP=��BEP=��EBC=90�㣬
���ı���EPCB�Ǿ��Σ�
��BE=PC��
��ABO=��BOC����BOC=��MPC��
$\left\{\begin{array}{l}{BE=CP}\\{��BEP=��BCP}\\{��ABO=��MPC}\end{array}\right.$
���BEF�ա�PCM��ASA����
����AOB����ƽ���˶���ʱ��Ϊt��s��ʱ��
BE=4-t��EP=3��AE=t��
���ı���EPCB�����Ϊ��3��4-t����
��ֱ��OB�Ľ���ʽΪy=kx������B��4��3������ã�
3=4k��
��ã�k=$\frac{3}{4}$��
��y=$\frac{3}{4}$x��
��F��t��$\frac{3}{4}$t����
��S��BEF=S��PCM=$\frac{1}{2}$��4-t����3-$\frac{3}{4}$t����
�ı���BFPM�����Ϊ��
S=3��4-t��-��4-t����3-$\frac{3}{4}$t��=$-\frac{3}{4}{t}^{2}+3t$
=$-\frac{3}{4}$��t-2��2+3����0��t��4����
��t=2ʱ��S�����ֵ�����ֵ��3��
��3���ٵ�OE=ECʱ��AE=OP=$\frac{1}{2}$OC=2��
�ڵ�OE=OC=4ʱ��AE2+OA2=OE2=OC2������t2+9=16��
��ã�t=$\sqrt{7}$��t=$-\sqrt{7}$���ᣩ��
�۵�EC=OC=4ʱ��
BE2+BC2=EC2��������4-t��2+9=16��
��ã�t=4+$\sqrt{7}$���ᣩ��t=4-$\sqrt{7}$��
��t=2��t=$\sqrt{7}$��t=4-$\sqrt{7}$��
��E����������2��3����$\sqrt{7}$��3����4-$\sqrt{7}$��3����
���� ������Ҫ�������ô���ϵ��������κ�����һ�κ����Ľ���ʽ���Լ�ƽ�Ƶ����ʣ�������ȫ�ȡ��������������֪ʶ�㣬���ƶ��ۺ��Ժ�ǿ����Ŀ����һ�����Ѷȣ�Ҫע�������ܽᣮ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
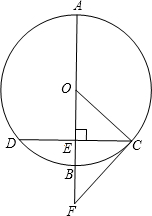 ��ͼ��AB�ǡ�O��ֱ������CD=2$\sqrt{5}$��AB��CD��E�㣬�ӳ�AB��F��ʹ��BF=$\frac{1}{2}$OB������CF����CF�ǡ�O�����ߣ���O�İ뾶��
��ͼ��AB�ǡ�O��ֱ������CD=2$\sqrt{5}$��AB��CD��E�㣬�ӳ�AB��F��ʹ��BF=$\frac{1}{2}$OB������CF����CF�ǡ�O�����ߣ���O�İ뾶���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
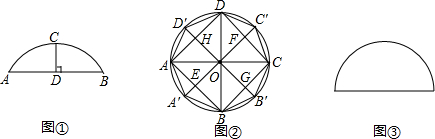
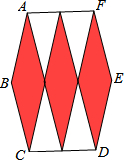 ��ͼ��3��ȫ�ȵ����ΰ���ͼ��ʽƴ����һ��ǡ�õõ�һ���߳���ȵ������Σ������νϳ��ĶԽ�����϶̵ĶԽ���֮���ǣ�������
��ͼ��3��ȫ�ȵ����ΰ���ͼ��ʽƴ����һ��ǡ�õõ�һ���߳���ȵ������Σ������νϳ��ĶԽ�����϶̵ĶԽ���֮���ǣ�������| A�� | $\sqrt{15}$ | B�� | $\sqrt{10}$ | C�� | 2$\sqrt{3}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
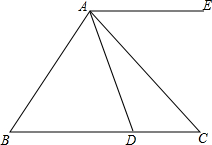 ��ͼ����֪�ڡ�ABC�У���ABC-��ACB=20�㣬��ACB�Ķ����ǡ�BAC������$\frac{1}{2}$��
��ͼ����֪�ڡ�ABC�У���ABC-��ACB=20�㣬��ACB�Ķ����ǡ�BAC������$\frac{1}{2}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com