
【题目】如图,O为直线AB上一点,∠BOC=36°.
(1)若OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数:
(2)若∠AOD=![]() ∠AOC,∠DOE=60°,如图(b)所示,求∠AOE的度数:
∠AOC,∠DOE=60°,如图(b)所示,求∠AOE的度数:
(3)若∠AOD=![]() ∠AOC,∠DOE=
∠AOC,∠DOE=![]() (n≥2,且n为正整数),如图(c)所示,请用n含的代数式表示∠AOE的度数__________(直接写出结果).
(n≥2,且n为正整数),如图(c)所示,请用n含的代数式表示∠AOE的度数__________(直接写出结果).
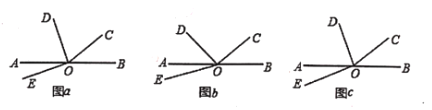
【答案】(1)18°;(2)12°;(3)![]() .
.
【解析】
(1)利用角平分线的性质得出∠AOD=∠DOC=72°,进而得出∠AOE的度数;
(2)设∠AOD=x,则∠DOC=2x,∠BOC=180°3x=36°,得出x的值,进而得出∠AOE的度数;
(3)利用(2)中作法,得出x与α的关系,进而得出答案.
解:(1)∵∠BOC=36°,OD平分∠AOC,
∴∠AOD=∠DOC=72°,
∵∠DOE=90°,则∠AOE=90°72°=18°;
故答案为:18°;
(2)设∠AOD=x,
则∠DOC=2x,
∠BOC=180°3x=36°,
解得:x=48°,
∴∠AOE=60°-x=60°48°=12°;
(3)设∠AOD=x,则∠DOC=(n1)x,∠BOC=180°-nx=36°,
解得:x=![]() ,
,
∴∠AOE=![]() -
-![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】在一次活动课上,第一小组同学把一个边长为1正方形纸片按如图方法剪裁:第一次剪成四个大小形状一样的小正方形,第二次将其中的一个小正方形再按向样的方法剪成四个小正方形,第三次再按同样的方法将其中一个小正方形剪成四个小正方形,如此循环进行下去.请你替他们完成下列问题:
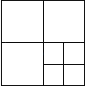
(1)完成表格:
剪的次数 | 1 | 2 | 3 | 4 | 5 | … |
正方形 个数 |
|
| 10 |
|
| … |
(2)如果剪了100次,共剪出 个小正方形;
(3)如果剪了n次,共剪出 个小正方形;
(4)如果剪了n次,则第n次得到的正方形边长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习千万条,思考第一条。请你用本学期所学知识探究以下问题:
(1)已知点![]() 为直线
为直线![]() 上一点,将直角三角板
上一点,将直角三角板![]() 的直角顶点放在点
的直角顶点放在点![]() 处,并在
处,并在![]() 内部作射线
内部作射线![]() .
.
①如图1,三角板的一边![]() 与射线
与射线![]() 重合,且
重合,且![]() ,若以点
,若以点![]() 为观察中心,射线
为观察中心,射线![]() 表示正北方向,求射线
表示正北方向,求射线![]() 表示的方向;
表示的方向;
②如图2,将三角板放置到如图位置,使![]() 恰好平分
恰好平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
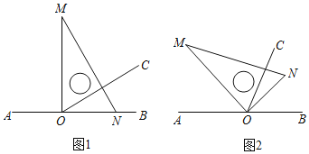
(2)已知点![]() 不在同一条直线上,
不在同一条直线上,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,用含
,用含![]() 的式子表示
的式子表示![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在生活中,人们经常通过一些标志性建筑确定位置,在数学中往往也是这样.
(1)将正整数如图1的方式进行排列:

小明同学通过仔细观察,发现每一行第一列的数字有一定的规律,所以每一行第一列的数字可以作为标志数,于是他认为第七行第一列的数字是 ,第7行、第5列的数字是 .
(2)方法应用
观察下面一列数:1,﹣2,3,﹣4,5,﹣6,7,…并将这列数按照如图2方式进行排列:
按照上述方式排列下去,
问题1:第10行从左边数第9个数是 ;
问题2:第n行有 个数;(用含n的代数式表示)
问题3:数字2019在第 行,从左边数第 个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠B=α,在AB,BC上分别找一点E,F,使△DEF的周长最小,此时,∠EDF=______。(用含α的代数式表示)
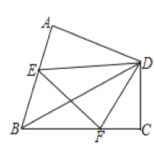
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
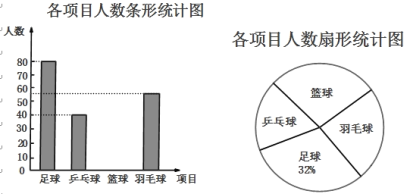
(1)这次活动一共调查了名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于多少度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一条自西向东的观光大道l上有A、B两个景点,A、B相距2km,在A处测得另一景点C位于点A的北偏东60°方向,在B处测得景点C位于景点B的北偏东45°方向,求景点C到观光大道l的距离.(结果精确到0.1km)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价不低于50元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件,设每件商品的售价为x元,每月的销售量为y件.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数形结合是数学解题中的一种重要思想,利用数轴可以将数与形完美结合.一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|,如:数轴上表示4和1的两点之间的距离是|4﹣1|=3;表示﹣3和2两点之间的距离是|﹣3﹣2|=5.
![]()
根据以上材料,结合数轴与绝对值的知识回答下列问题:
(1)将数﹣5,﹣![]() ,0,2.5在数轴上表示出来.
,0,2.5在数轴上表示出来.
(2)若数轴上表示数a的点位于﹣3与2之间,那么|a+3|+|a﹣2|的值是多少?
(3)若A是数轴上的一个点,它表示数a,则|a+5|+|a﹣3|的最小值是多少?当a取多少时|a+5|+|a﹣1|+|a﹣3|有最小值?最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com