
 ,0),则有a+3=
,0),则有a+3=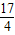 ,即可求出a的值.
,即可求出a的值. 则A′的坐标为(2,3),把A′向右平移3个单位得到点B'(5,3),连接BB′,与x轴交于点D,如图,
则A′的坐标为(2,3),把A′向右平移3个单位得到点B'(5,3),连接BB′,与x轴交于点D,如图,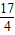 ,
,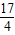 ,0),
,0), ,
, .
. .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2012年初中毕业升学考试(四川巴中卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,一次函数 的图象与y轴交于点A,
的图象与y轴交于点A,
与x轴交于点B,与反比例函数 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出 时x的取值范围。
时x的取值范围。

查看答案和解析>>
科目:初中数学 来源:2013届安徽滁州八年级下期末模拟数学试卷(沪科版)(解析版) 题型:解答题
已知:如图1,平面直角坐标系 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐
标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com