
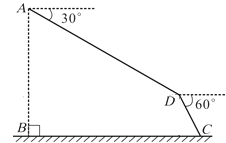
【题目】2017年9月8日—10日,第六届翼装飞行世界锦标赛在我市天门山风景区隆重举行,来自全球11个国家的16名选手参加了激烈的角逐.如图,某选手从离水平地面1000米高的A点出发(AB=1000米),沿俯角为![]() 的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为
的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为![]() 的方向降落到地面上的C点,求该选手飞行的水平距离
的方向降落到地面上的C点,求该选手飞行的水平距离![]() .
.

【答案】![]()
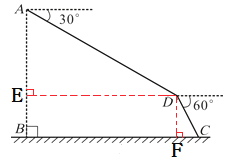
【解析】如图,作DE⊥AB于E,DF⊥BC于F,根据题意得到∠ADE=30°,∠CDF=30°,利用含30度的直角三角形三边的关系计算出AE=![]() AD=700,DE=
AD=700,DE=![]() AE=700
AE=700![]() ,则BE=300,所以DF=300,BF=700
,则BE=300,所以DF=300,BF=700![]() ,再在Rt△CDF中计算出CF,然后计算BF和CF的和即可.
,再在Rt△CDF中计算出CF,然后计算BF和CF的和即可.
如图,作DE⊥AB于E,DF⊥BC于F,∠ADE=30°,∠CDF=30°,
在Rt△ADE中,AE=![]() AD=
AD=![]() ×1400=700,
×1400=700,
DE=![]() AE=700
AE=700![]() ,
,
∴BE=AB-AE=1000-700=300,
∴DF=300,BF=700![]() ,
,
在Rt△CDF中,CF=![]() DF=
DF=![]() ×300=100
×300=100![]() ,
,
∴BC=700![]() +100
+100![]() =800
=800![]() .
.
答:选手飞行的水平距离BC为800![]() m.
m.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】观察以下等式:![]()
将以上三个等式两边分别相加得:![]()
(1)猜想并写出:![]() ____________.
____________.
(2)直接写出下列各式的计算结果:
①![]() _____________;
_____________;
②![]() ___________.
___________.
(3)探究并计算:![]()
(4)![]() ___________.
___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人准备在一段长为1200m的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100m处,两人同时起跑.
(1)两人出发后多长时间乙追上甲?
(2)求从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y(m)与时间t(s)的函数关系,并画出y(m)与时间t(s)的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
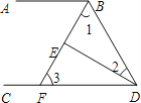
【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣![]() x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=![]() x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )

A. 当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m
B. 小球距O点水平距离超过4米呈下降趋势
C. 小球落地点距O点水平距离为7米
D. 斜坡的坡度为1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
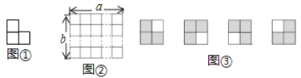
【题目】用若干个形状、大小完全相同的矩形纸片围成正方形,4个矩形纸片围成如图①所示的正方形,其阴影部分的面积为12;8个矩形纸片围成如图②所示的正方形,其阴影部分的面积为8;12个矩形纸片围成如图③所示的正方形,其阴影部分的面积为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读思考,完成下列填空.
问题提出:
如图,图①是一张由三个边长为1的小正方形组成的![]() 形纸片.图②是张
形纸片.图②是张![]() 的方格纸(
的方格纸(![]() 的方格纸指边长分别为
的方格纸指边长分别为![]() 的长方形,被分成
的长方形,被分成![]() 个边长为1的小正方形,其中
个边长为1的小正方形,其中![]() ,且
,且![]() 为正整数).把图①放置在图②中.使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
为正整数).把图①放置在图②中.使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
问题探究;
探究一:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,如图③,显然有4种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,如图③,显然有4种不同的放置方法.
探究二:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形.如图④,在
的方格纸中,使它恰好盖住其中的三个小正方形.如图④,在![]() 的方格纸中,共可以找到2个位置不同的
的方格纸中,共可以找到2个位置不同的![]() 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在![]() 的方格纸中.使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.
的方格纸中.使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.
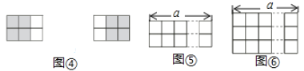
探究三:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,如图⑤,在
的方格纸中,使它恰好盖住其中的三个小正方形,如图⑤,在![]() 的方格纸中,共可以找到_______个位置不同的
的方格纸中,共可以找到_______个位置不同的![]() 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,共有________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,共有________种不同的放置方法.
探究四:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,如图⑥,在
的方格纸中,使它恰好盖住其中的三个小正方形,如图⑥,在![]() 的方格纸中,共可以找到_______个位置不同的
的方格纸中,共可以找到_______个位置不同的![]() 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形共有________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形共有________种不同的放置方法.
……
问题解决:
把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,共有_________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,共有_________种不同的放置方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
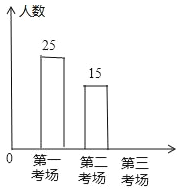
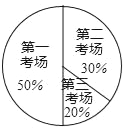
【题目】2017年12月全市组织了计算机等级考试,江南中学九(1)班同学都参加了计算机等级考试,分第一试场、第二试场、第三试场,下面两幅统计图反映原来安排九(1)班考生人数,请你根据图中的信息回答下列问题:
(1)该班参加第三试场考试的人数为_____,并补全频数分布直方图;
(2)根据实际情况,需从第一试场调部分学生到第三试场考试,使第一试场的人数与第三试场的人数比为2:3,应从第一试场调多少学生到第三试场?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com