
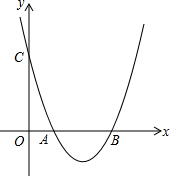
 已知二次函数y=a(x-1)(x-3)(a>0)的图象与x轴交于A、B两点(A左B右),与y轴交于C点(0,3).P为x轴下方二次函数y=a(x-1)(x-3)(a>0)图象上一点,P点横坐标为m.
已知二次函数y=a(x-1)(x-3)(a>0)的图象与x轴交于A、B两点(A左B右),与y轴交于C点(0,3).P为x轴下方二次函数y=a(x-1)(x-3)(a>0)图象上一点,P点横坐标为m.分析 (1)把C(0,3)代入y=a(x-1)(x-3)即可求出a解决问题;
(2)如图1中,连接AC、PC、BC、PB.首先利用勾股定理等逆定理证明△PBC是直角三角形,由tan∠PCB=$\frac{BP}{BC}=\frac{{\sqrt{2}}}{{3\sqrt{2}}}=\frac{1}{3}$,tann∠ACO=$\frac{OA}{OC}=\frac{1}{3}$,推出tan∠PCB=tan∠ACO,即可解决问题;
(3)分两种情形求解即可(ⅰ)如图2中,当点Q在BC左侧的抛物线上时.(ⅱ)如图3中,当点Q在BC右侧的抛物线上时,延长CQ交x轴于点E,过点E作EF⊥CB交CB的延长线于点F.分别构建方程即可解决问题.
解答 解:(1)把C(0,3)代入y=a(x-1)(x-3)得到3a=3,
∴a=1,
∴a的值为1;
(2)如图1中,连接AC、PC、BC、PB.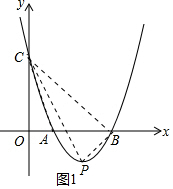
∵a=1
∴抛物线的解析式为:y=(x-1)(x-3)=x2-4x+3=(x-2)2-1
∴P(2,-1)
∵B(3,0),C(0,3)
∴CP=$2\sqrt{5}$,BP=$\sqrt{2}$,CB=$3\sqrt{2}$
∴BP2+BC2=20,$C{P^2}={(2\sqrt{5})^2}=20$
∴BP2+BC2=CP2
∴∠CBP=90°
∴tan∠PCB=$\frac{BP}{BC}=\frac{{\sqrt{2}}}{{3\sqrt{2}}}=\frac{1}{3}$
∵tan∠ACO=$\frac{OA}{OC}=\frac{1}{3}$
∴tan∠PCB=tan∠ACO
∴∠ACO=∠PCB;
(3)(ⅰ)如图2中,当点Q在BC左侧的抛物线上时,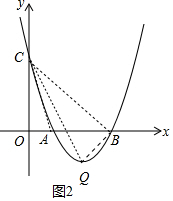
由(2)可知Q(2,-1)
∴m+n=2
∵P为x轴下方二次函数y=x2-4x+3图象上一点,
∴1<m<3
∴1<2-n<3
∴-1<n<1;
(ⅱ)如图3中,当点Q在BC右侧的抛物线上时,延长CQ交x轴于点E,过点E作EF⊥CB交CB的延长线于点F.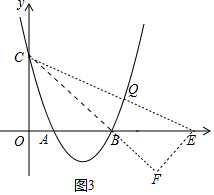
∵∠ACO=∠QCB
∴tan∠ACO=tan∠QCB
∴$\frac{OA}{OC}=\frac{EF}{CF}$
设EF长为x
∴$\frac{1}{3}=\frac{x}{{x+3\sqrt{2}}}$
解得:$x=\frac{3}{2}\sqrt{2}$
∴BE=3
∴E(6,0)
∴CE的解析式为:y=-$\frac{1}{2}$x+3,
由$\left\{\begin{array}{l}y=-\frac{1}{2}x+3\\ y={x^2}-4x+3\end{array}\right.$解得$\left\{\begin{array}{l}{x_1}=\frac{7}{2}\\{y_1}=\frac{5}{4}\end{array}\right.$,$\left\{\begin{array}{l}{x_2}=0\\{y_2}=3\end{array}\right.$
∴Q$(\frac{7}{2},\frac{5}{4})$,
∴m+n=$\frac{7}{2}$
∵1<m<3
∴1<$\frac{7}{2}$-n<3
∴$\frac{1}{2}<n<\frac{5}{2}$
综上所述:n的取值范围是-1<n<1或$\frac{1}{2}<n<\frac{5}{2}$即-1<n<$\frac{5}{2}$.
点评 本题考查二次函数综合题、一次函数的应用、锐角三角函数、勾股定理以及逆定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
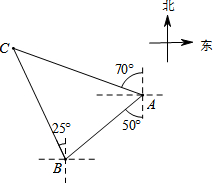 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )| A. | 10$\sqrt{2}$海里 | B. | 10$\sqrt{3}$海里 | C. | 10$\sqrt{6}$海里 | D. | 20$\sqrt{6}$海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
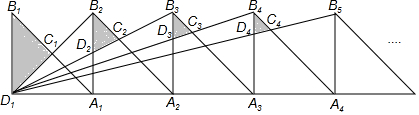
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
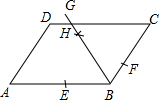 如图,在?ABCD中,AB>2BC,观察图中尺规作图的痕迹,则下列结论错误的是( )
如图,在?ABCD中,AB>2BC,观察图中尺规作图的痕迹,则下列结论错误的是( )| A. | BG平分∠ABC | B. | BE=BF | C. | AD=CH | D. | CH=DH |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com