
【题目】对二次函数y=x2+2mx+1,当0<x≤4时函数值总是非负数,则实数m的取值范围为_____.
【答案】当m≥﹣1时,当0<x≤4时函数值总是非负数
【解析】
分三种情况讨论:①当对称轴x<0时,即﹣m<0,m>0,满足当0<x≤4时的函数值总是非负数;②当![]() 时,0≤﹣m<4,﹣4<m≤0,当1﹣m2≥0时,﹣1≤m≤1,满足当0<x≤4时的函数值总是非负数;③当对称轴﹣m≥4,即m≤﹣4,如果满足当0<x≤4时的函数值总是非负数,则有x=4时,y≥0.
时,0≤﹣m<4,﹣4<m≤0,当1﹣m2≥0时,﹣1≤m≤1,满足当0<x≤4时的函数值总是非负数;③当对称轴﹣m≥4,即m≤﹣4,如果满足当0<x≤4时的函数值总是非负数,则有x=4时,y≥0.
解:对称轴为:![]() ,
,![]()
分三种情况:①当对称轴x<0时,即﹣m<0,m>0,满足当0<x≤4时的函数值总是非负数;
②当![]() 时,0≤﹣m<4,﹣4<m≤0,当1﹣m2≥0时,﹣1≤m≤1,满足当0<x≤4时的函数值总是非负数;
时,0≤﹣m<4,﹣4<m≤0,当1﹣m2≥0时,﹣1≤m≤1,满足当0<x≤4时的函数值总是非负数;
当1﹣m2<0时,不能满足当0<x≤4时的函数值总是非负数;
∴当﹣1≤m≤0时,当0<x≤4时的函数值总是非负数,
③当对称轴﹣m≥4,即m≤﹣4,如果满足当0<x≤4时的函数值总是非负数,则有x=4时,y≥0,
16+4m+1≥0,
m≥﹣![]() ,此种情况m无解;
,此种情况m无解;
综合可得:当m≥﹣1时,当0<x≤4时函数值总是非负数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
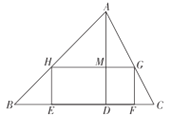
【题目】如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E,F在BC上,AD交HG于点M.
(1)设矩形EFGH的长HG=ycm,宽HE=xcm.求y与x的函数关系式;
(2)当x为何值时,矩形EFGH的面积S最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“某市为处理污水,需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时×××××.设原计划每天铺设管道x米,则可得方程![]() .”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
.”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
A.每天比原计划多铺设10米,结果延期20天才完成任务
B.每天比原计划少铺设10米,结果延期20天才完成任务
C.每天比原计划多铺设10米,结果提前20天完成任务
D.每天比原计划少铺设10米,结果提前20天完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
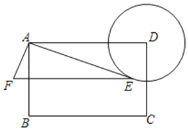
【题目】如图,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,使∠EAF=90°,tan∠AEF=![]() ,则点F与点C的最小距离为_____.
,则点F与点C的最小距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
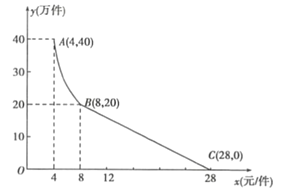
【题目】“净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上(![]() ),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
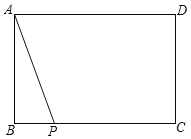
【题目】如图,已知矩形ABCD中,AB=3,BC=5,P是线段BC上的一动点.
(1)请用不带刻度的直尺和圆规,按下列要求作图:(不要求写作法,但保留作图痕迹),在CD边上确定一点E,使得∠DEP+∠APB=180°;
(2)在(1)的条件下,点P从点B移动到点C的过程中,对应点E随之运动,则移动过程中点E经过的总路程长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
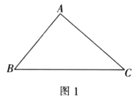
(1)如图1,已知三角形![]() ,请在
,请在![]() 边上确定一点
边上确定一点![]() ,使得
,使得![]() 的值最小.
的值最小.
问题探究
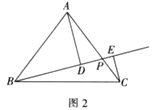
(2)如图2,在等腰![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一动点,分别过点
边上一动点,分别过点![]() ,点
,点![]() 作线段
作线段![]() 所在直线的垂线,垂足为点
所在直线的垂线,垂足为点![]() ,若
,若![]() ,求线段
,求线段![]() 的取值范围,并求
的取值范围,并求![]() 的最大值.
的最大值.
问题解决
(3)如图3,正方形![]() 是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点
是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点![]() 处和
处和![]() 边的两个三等分点
边的两个三等分点![]() 之间的某点
之间的某点![]() 建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为
建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为![]() 、
、![]() 、
、![]() .若你是此次项目设计的负责人,要使三条运输轨道的距离之和
.若你是此次项目设计的负责人,要使三条运输轨道的距离之和![]() 最小,你能不能按照要求进行规划,请通过计算说明.
最小,你能不能按照要求进行规划,请通过计算说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
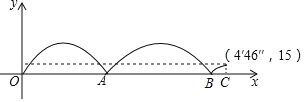
【题目】某中学举办运动会,在1500米的项目中,参赛选手在200米的环形跑道上进行,如图记录了跑的最快的一位选手与最慢的一位选手的跑步过程(最快的选手跑完了全程),其中x表示最快的选手的跑步时间,y表示这两位选手之间的距离,现有以下4种说法,正确的有( )
①最快的选手到达终点时,最慢的选手还有15米未跑;
②跑的最快的选手用时4'46″;
③出发后最快的选手与最慢的选手相遇了两次;
④出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时长.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
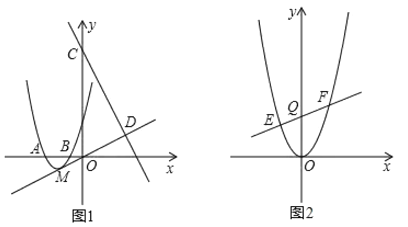
【题目】如图(1),抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点.
(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=-2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围;
(3)如图(2),将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于E,F两点.问在y轴的负半轴上是否存在点P,使△PEF的内心在y轴上.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com