
【题目】如图,在梯形ABCD中, ![]() ,
,![]() ,求DC的长.
,求DC的长.
【答案】解:如图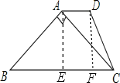
过A作AE⊥BC于E,过D作DF⊥BC于F,
则∠AEF=∠DFE=∠DFC=∠AEB=90°,AE∥DF,
∵AD∥BC,
∴四边形AEFD是矩形,
∴AE=DF,AD=EF=![]() ,
,
在Rt△BAC中,∠B=45°,BC=![]() ,
,
∴∠ACB=45°=∠B,
∴AB=AC,
由勾股定理得:AB=AC=4,
△BAC的面积S=![]() AB×AC=
AB×AC=![]() BC×AE,
BC×AE,
∴AE=![]()
DF=AE=![]() ,
,
∵AB=AC,AE⊥BC,
∴BE=CE=![]() BC=
BC=![]() ,
,
∴CF=![]() -
-![]() =
=![]() ,
,
在Rt△DFC中,DF=![]() ,CF=
,CF=![]() , 由勾股定理得:CD=
, 由勾股定理得:CD=![]()
【解析】过A作AE⊥BC于E,过D作DF⊥BC于F,得出矩形AEFD,求出AE=DF,AD=EF,求出AE、EC的长,求出CF长,即可求出答案.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,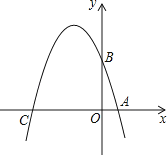
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx的图象经过点(2,0)、(﹣1,6).
(1)求二次函数的解析式;
(2)画出它的图象;
(3)写出它的对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)11![]() -1
-1![]() -1
-1![]() +4
+4![]() ;
;
(2)(-22.84)-(+38.57)+(-37.16)-(-32.57);
(3)1![]() -
-![]() +2
+2![]() +
+![]() -4
-4![]() ;
;
(4)(-36)-(-28)+(+125)+(-4)-(+53)-(-40).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,对角线AC和BD交于点O,下列条件中,能判断梯形ABCD是等腰梯形的是( )
A.∠BDC =∠BCD
B.∠ABC =∠DAB
C.∠ADB =∠DAC
D.∠AOB =∠BOC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上以每秒
边上以每秒![]() 的速度从点
的速度从点![]() 向点
向点![]() 运动,点
运动,点![]() 在
在![]() 边上,以每秒
边上,以每秒![]() 的速度从点
的速度从点![]() 出发,在
出发,在![]() 间往返运动,两个点同时出发,当点
间往返运动,两个点同时出发,当点![]() 到达点
到达点![]() 时停止(同时点
时停止(同时点![]() 也停止).设运动时间为
也停止).设运动时间为![]() 秒,当
秒,当![]() 为何值时,以点
为何值时,以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?
为顶点的四边形是平行四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )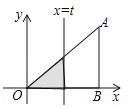
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在⊙O中. AE直径,AD是弦,B为AE延长线上--点,作BC⊥AD,与AD延长线交于点C.且∠CBD=∠A.
(1)判断直线BD与⊙0的位置关系,并证明你的结论;
(2)若∠A=30 ![]() ,OA=6,求图中阴影部分的面积.
,OA=6,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com