练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．下列判断正确的是（　　）
    A．两条直线被第三条直线所截，同位角相等
    B．在同一平面内，a⊥b，b⊥c，则c⊥a
    C．同旁内角互补，则它们的角平分线互相垂直
    D．经过一点有且只有一条直线与已知直线平行

    分析 A、由“两直线平行，同位角相等”即可得出A不符合题意；B、由“在同一平面内，a⊥b，b⊥c，则a∥c”即可得出B不符合题意；C、由“同旁内角互补，则它们的角平分线互相垂直”即可得出C符合题意；D、由“过直线外一点有且只有一条直线与已知直线平行”即可得出D不符合题意．综上即可得出结论．

    解答 解：A、两条平行直线被第三条直线所截，同位角相等，故A不符合题意；
    B、在同一平面内，a⊥b，b⊥c，则a∥c，故B不符合题意；
    C、同旁内角互补，则它们的角平分线互相垂直，故C符合题意；
    D、经过直线外一点有且只有一条直线与已知直线平行，故D不符合题意．
    故选C．

    点评 本题考查了平行线的判定与性质以及平行公理及推论，逐一分析四个选项的正误是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．先化简，再求值：$（1-\frac{2}{a}）÷\frac{{{a^2}-4a+4}}{{{a^2}-4}}-\frac{a+4}{a+2}$，其中a满足a2+2a-15=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．定义一种新的运算“※”，规定：x※y=mx+ny2，其中m、n为常数，已知2※3=-1，3※2=8，则m※n=15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，A、B、C是⊙O上三点，∠OAB=65°，则∠ACB的度数是25°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．在代数式$\frac{2}{x}$，$\frac{1}{3}$（x+y），$\frac{x}{π-2}$，$\frac{5}{a-x}$，$\frac{{x}^{2}}{x}$中，分式有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．先化简，再求值：[（5m-3n）（m+4n）-5m（m+4n）]÷3n（m=2，n=-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

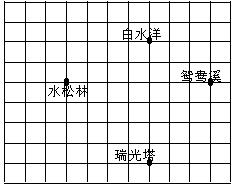    10．暑假时小明和小颖到福建屏南旅游，小明在如上图所示的旅游简图上建立了直角坐标系，但他只告诉小颖白水洋的坐标是（2，5），请你帮小颖写出鸳鸯溪的坐标是（5，3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列各式不是一元一次不等式组的是（　　）
    A．$\left\{\begin{array}{l}x＞3\\ x＜1\end{array}\right.$B．$\left\{\begin{array}{l}3x＜5\\ 2x-1＜9\end{array}\right.$C．$\left\{\begin{array}{l}x-1＞3\\ y+2＜1\end{array}\right.$D．$\left\{\begin{array}{l}x-1＞3\\ x-3＜2\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．化简求值：
    （1）（a+b）（a-b）+（a+b）2，其中a=3，b=-$\frac{1}{3}$．
    （2）已知2x-y=10，求[（x2+y2）-（x-y）2+2y（x-y）]÷4y的值．

    查看答案和解析>>

    同步练习册答案