已知关于x的不等式ax+3>0(其中a≠0).
(1)当a=-2时,求此不等式的解,并在数轴上表示此不等式的解集;
(2)小明准备了十张形状、大小完全相同的不透明卡片,上面分别写有整数:-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,将这10张卡片写有整数的一面向下放在桌面上.从中任意抽取一张,以卡片上的数作为不等式中的系数a,求使该不等式没有正整数解的概率.
【答案】
分析:(1)把a的值代入就得到不等式,从而可以求出解集;
(2)每个数字被抽到的机会相同,共有10个不同的结果,然后确定以卡片上的数作为不等式中的系数a,求使该不等式没有正整数解的a的值有几个,用这个数除以10就得到概率.
解答:解:(1)把a=-2代入不等式得
-2x+3>0
解得x<

.
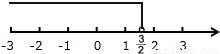
(2)∵ax+3>0(a≠0)的解集为x<-

,
若要使不等式没有正整数解,则-

≤1,即a≤-3,
∴在这10个数中,能使不等式没有正整数解的a的值有-10,-9,-8,-7,-6,-5,-4,-3共8个
∴该不等式没有正整数解的概率为

=

.
点评:主要考查了一元一次不等式的解法和其特殊值的求法.
解不等式要用到不等式的性质:
(1)不等式的两边加(或减)同一个数(或式子),不等号的方向不变;
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;
(3)不等式的两边乘(或除以)同一个负数,不等号的方向改变.用到的知识点为:概率=所求情况数与总情况数之比.

 .
.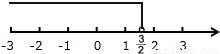
 ,
, ≤1,即a≤-3,
≤1,即a≤-3, =
= .
.

 阅读快车系列答案
阅读快车系列答案