
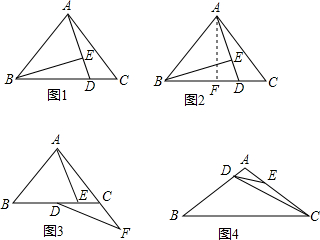
分析 (1)作AF⊥BC,判断出△ABF≌△BAE(AAS),得出BF=AE,即可;
(2)先求出tan∠DAE=$\frac{1}{2}$,再由tan∠F=tan∠DAE,求出CG,最后用△DCG∽△ACE求出AC;
(3)构造含30°角的直角三角形,设出DG,在Rt△ABH,Rt△ADN,Rt△ABH中分别用a,k表示出AB=2a(k+1),BH=$\sqrt{3}$a(k+1),BC=2BH=2$\sqrt{3}$a(k+1),CG=$\sqrt{3}$a(2k+1),DN=$\sqrt{3}$ka,最后用△NDE∽△GDC,求出AE,EC即可.
解答 证明:(1)如图2,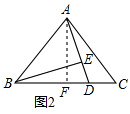
作AF⊥BC,
∵BE⊥AD,∴∠AFB=∠BEA,
在△ABF和△BAE中,
$\left\{\begin{array}{l}{∠AFB=∠BEA}\\{∠DAB=∠ABD}\\{AB=AB}\end{array}\right.$,
∴△ABF≌△BAE(AAS),
∴BF=AE
∵AB=AC,AF⊥BC,
∴BF=$\frac{1}{2}$BC,
∴BC=2AE,
故答案为AAS
(2)如图3,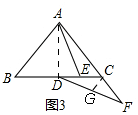
连接AD,作CG⊥AF,
在Rt△ABC中,AB=AC,点D是BC中点,
∴AD=CD,
∵点E是DC中点,
∴DE=$\frac{1}{2}$CD=$\frac{1}{2}$AD,
∴tan∠DAE=$\frac{DE}{AD}$=$\frac{\frac{1}{2}CD}{AD}$=$\frac{1}{2}$,
∵AB=AC,∠BAC=90°,点D为BC中点,
∴∠ADC=90°,∠ACB=∠DAC=45°,
∴∠F+∠CDF=∠ACB=45°,
∵∠CDF=∠EAC,
∴∠F+∠EAC=45°,
∵∠DAE+∠EAC=45°,
∴∠F=∠DAE,
∴tan∠F=tan∠DAE=$\frac{1}{2}$,
∴$\frac{CG}{CF}=\frac{1}{2}$,
∴CG=$\frac{1}{2}$×2=1,
∵∠ACG=90°,∠ACB=45°,
∴∠DCG=45°,
∵∠CDF=∠EAC,
∴△DCG∽△ACE,
∴$\frac{DC}{AC}=\frac{CG}{CE}$,
∵CD=$\frac{\sqrt{2}}{2}$AC,CE=$\frac{1}{2}$CD=$\frac{\sqrt{2}}{4}$AC,
∴$\frac{\frac{\sqrt{2}}{2}AC}{AC}=\frac{1}{\frac{\sqrt{2}}{4}AC}$,
∴AC=4;
∴AB=4;
(3)如图4,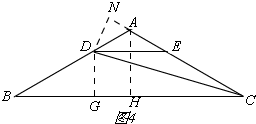
过点D作DG⊥BC,设DG=a,
在Rt△BGD中,∠B=30°,
∴BD=2a,BG=$\sqrt{3}$a,
∵AD=kDB,
∴AD=2ka,AB=BD+AD=2a+2ka=2a(k+1),
过点A作AH⊥BC,
在Rt△ABH中,∠B=30°.
∴BH=$\sqrt{3}$a(k+1),
∵AB=AC,AH⊥BC,
∴BC=2BH=2$\sqrt{3}$a(k+1),
∴CG=BC-BG=$\sqrt{3}$a(2k+1),
过D作DN⊥AC交CA延长线与N,
∵∠BAC=120°,
∴∠DAN=60°,
∴∠ADN=30°,
∴AN=ka,DN=$\sqrt{3}$ka,
∵∠DGC=∠AND=90°,∠AED=∠BCD,
∴△NDE∽△GDC.
∴$\frac{DN}{DG}=\frac{NE}{CG}$,
∴$\frac{\sqrt{3}ka}{a}=\frac{NE}{\sqrt{3}a(2k+1)}$,
∴NE=3ak(2k+1),
∵AN=ka,
∴AE=NE-AN=2ak(3k+1),
∴EC=AC-AE=AB-AE=2a(k+1)-2ak(3k+1)=2a(1-3k2),
∴$\frac{AE}{EC}=\frac{2ak(3k+1)}{2a(1-3{k}^{2})}$=$\frac{3{k}^{2}+k}{1-3{k}^{2}}$.
点评 此题是相似形综合题,主要考查了全等三角形的判定和性质,相似三角形的性质和判定,等腰三角形的性质,等腰直角三角形的性质,中点的定义,解本题的关键是作出辅助线,也是本题的难点.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | (a-10%)(a+15%)万元 | B. | a(1-90%)(1+85%)万元 | C. | a(1-10%)(1+15%)万元 | D. | a(1-10%+15%)万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2020 | 3000 |
| 发芽的频数m | 96 | 283 | 344 | 552 | 948 | 1912 | 2848 |
| 发芽的频率 | 0.96 | 0.94 | 0.86 | 0.92 | 0.95 | 0.95 | 0.95 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y1>y3>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明参加某超市的翻笑脸抽奖活动,如图,四张笑脸背后分别对应价值50,100,100,200(单位:元)的代金券
小明参加某超市的翻笑脸抽奖活动,如图,四张笑脸背后分别对应价值50,100,100,200(单位:元)的代金券查看答案和解析>>
科目:初中数学 来源: 题型:填空题
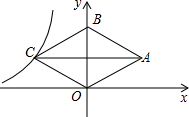 如图,菱形OABC的顶点O是原点,顶点B在y轴上,已知菱形的边长为5,一条对角线的长是6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过顶点C,则k的值为-12.
如图,菱形OABC的顶点O是原点,顶点B在y轴上,已知菱形的边长为5,一条对角线的长是6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过顶点C,则k的值为-12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com