
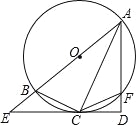
【题目】如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC、CF.
(1)求证:CD是⊙O的切线;
(2)若AD=6,DE=8,求BE的长;
(3)求证:AF+2DF=AB.
【答案】(1)证明详见解析;(2) ![]() ;(3)证明详见解析.
;(3)证明详见解析.
【解析】
试题分析:(1)连接OC,由AB为⊙O的直径,得到∠ACB=90°,求得∠ACB=∠D,根据角平分线的性质得到∠BAC=∠CAD,通过相似三角形得到∠ABC=∠ACD,等量代换得到∠OCB=∠ACD,求出∠OCD=90°,即可得到结论;
(2)根据勾股定理得到AE=![]() =10,根据相似三角形的性质得到
=10,根据相似三角形的性质得到![]() ,代入数据得到r=
,代入数据得到r=![]() ,于是得到结论;
,于是得到结论;
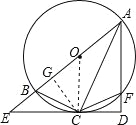
(3)过C作 CG⊥AE于G,根据全等三角形的性质得到AG=AD,CG=CD,推出Rt△BCG≌Rt△FCD,由全等三角形的性质得到BG=FD,等量代换即可得到结论.
试题解析:(1)连接OC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵CD⊥AF,
∴∠D=90°,
∴∠ACB=∠D,
∵AC平分∠BAF,
∴∠BAC=∠CAD,
∴△ABC∽△ACD,
∴∠ABC=∠ACD,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠ACD,
∵∠OCB+∠ACO=∠ACO+∠ACD=90°,
∴∠OCD=90°,
∴CD是⊙O的切线;
(2)∵AD=6,DE=8,
∴AE=![]() =10,
=10,
∵OC∥AD,
∴∠OCE=∠ADE,
∴△OCE∽△ADE,
∴![]() ,即
,即![]() ,
,
∴r=![]() ,
,
∴BE=10﹣![]() =
=![]() ;
;
(3)过C作 CG⊥AE于G,
在△ACG与△ACD中,
∠GAC=∠DAC,∠CGA=∠CDA,AC=AC,
∴△ACG≌△ACD,
∴AG=AD,CG=CD,
∵BC=CF,
在Rt△BCG与Rt△FCD中,
CG=CD,BC=CF,
∴Rt△BCG≌Rt△FCD,
∴BG=FD,
∴AF+2DF=AD+DF=AG+GB=AB,
即AF+2DF=AB.


科目:初中数学 来源: 题型:
【题目】连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是( ).
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
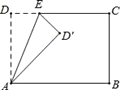
【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=9,AB=CD=15.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B、C在数轴上表示的数a、b、c满足(b+3)2+|c﹣24|=0,且多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式.
(1)分别求a、b、c的值;
(2)已知点P、点Q是数轴上的两个动点,点P从点A出发,以3个单位/秒的速度向右运动,同时点Q从点C出发,以7个单位/秒的速度向左运动:
①若点P和点Q经过t秒后在数轴上的点D处相遇,求出t的值和点D所表示的数;
②若点P运动到点B处,动点Q再出发,则P运动几秒后这两点之间的距离为5个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时刻,单位时间进出路口A,B,C的机动车辆数如图所示.图中x1 , x2 , x3分别表示该时段单位时间通过路段AB,BC,CA的机动车辆数(假设单位时间内在上述路段中同一路段上驶入与驶出的车辆数相等),则有( ) 
A.x1>x2>x3
B.x1>x3>x2
C.x2>x3>x1
D.x3>x2>x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽做一道数学题:“已知两个多项式A,B,B为 ![]() ﹣5x﹣6,求A+B”.小丽把A+B看成A﹣B,计算结果是
﹣5x﹣6,求A+B”.小丽把A+B看成A﹣B,计算结果是 ![]() +10x+12.根据以上信息,你能求出A+B的结果吗?
+10x+12.根据以上信息,你能求出A+B的结果吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com