

科目:初中数学 来源: 题型:
| 2 |
| 2 |
3
| ||
| 2 |
| ||
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 初始问题:如图1,已知两个同心圆,直线AD分别交大⊙O于点A、D,交小⊙O于点B、C.
初始问题:如图1,已知两个同心圆,直线AD分别交大⊙O于点A、D,交小⊙O于点B、C.| MN | PQ |
查看答案和解析>>
科目:初中数学 来源: 题型:

 (用含∠α的式子表示);
(用含∠α的式子表示);查看答案和解析>>
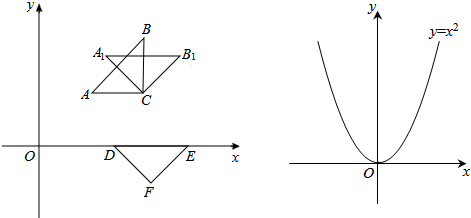
科目:初中数学 来源:2013年浙江省义乌市中考数学试卷(解析版) 题型:解答题
 ,0),E(2
,0),E(2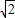 ,0),F(
,0),F(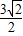 ,-
,-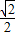 ).
). x2+bx+c上,请你求出符合条件的抛物线解析式;
x2+bx+c上,请你求出符合条件的抛物线解析式;
查看答案和解析>>
科目:初中数学 来源:2011-2012年北京昌平区九年级第一学期期末考试数学卷 题型:解答题
【初始问题】如图1,已知两个同心圆,直线AD分别交大⊙O于点A、D,交小⊙O于点B、C.AB与CD相等吗?请证明你的结论.
【类比研究】如图2,若两个等边三角形ABC和A1 B1 C1的中心(点O)相同,且满足AB∥A1B1,BC∥B1C1,AC∥A1C1,可知AB与A1B1,BC与B1C1,AC与A1C1之间的距离相等.直线MQ分别交三角形的边于点M、N、P、Q,与AB所成夹角为∠α(30°<∠α<90°).

1.(1)求 (用含∠α的式子表示);
(用含∠α的式子表示);
2.(2)求∠α等于多少度时,MN = PQ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com