
|
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:
 ,其图象为如图所示的一段曲线,且端点为 ,其图象为如图所示的一段曲线,且端点为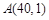 和 和 ,若行驶速度不得超过60(km/h),则汽车通过该路段最少需要时间为( ) ,若行驶速度不得超过60(km/h),则汽车通过该路段最少需要时间为( )
|
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源:不详 题型:解答题
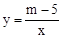 (m为常数)图象的一支.
(m为常数)图象的一支.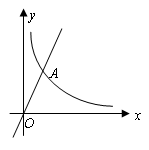
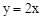 图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
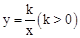 与它的其中一条对称轴
与它的其中一条对称轴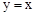 相交于两点A,B,则线段AB的长称为双曲线
相交于两点A,B,则线段AB的长称为双曲线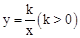 的对径.
的对径.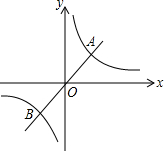
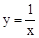 的对径;
的对径;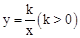 对径是
对径是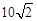 .求k的值;
.求k的值;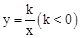 的对径.
的对径.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
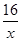 在第一象限图像上,点A1、A2……An在X轴上,若△P1OA1、△P2A1A2……△PnAN-1AN均为等腰直角三角形,则:
在第一象限图像上,点A1、A2……An在X轴上,若△P1OA1、△P2A1A2……△PnAN-1AN均为等腰直角三角形,则: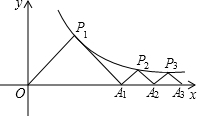
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
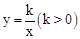 在第一象限图像上的一点,点A1的坐标为(2,0).若△P1O A1与△P2 A1 A2均为等边三角形,则A2点的横坐标为
在第一象限图像上的一点,点A1的坐标为(2,0).若△P1O A1与△P2 A1 A2均为等边三角形,则A2点的横坐标为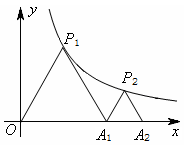
A.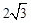 | B.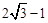 | C.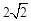 | D.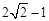 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com