
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
科目:初中数学 来源: 题型:选择题
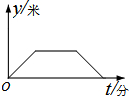 李阿姨每天早晨从家慢跑道小区公园,锻炼一阵后,再慢跑回家.表示李阿姨离开家的距离y (单位:米)与时间t (单位:分)的函数关系的图象大致如上图所示,则李阿姨跑步的路线可能是(用P点表示李阿姨家的位置)( )
李阿姨每天早晨从家慢跑道小区公园,锻炼一阵后,再慢跑回家.表示李阿姨离开家的距离y (单位:米)与时间t (单位:分)的函数关系的图象大致如上图所示,则李阿姨跑步的路线可能是(用P点表示李阿姨家的位置)( )| A. | 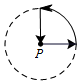 | B. | 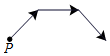 | C. | 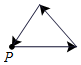 | D. | 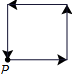 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
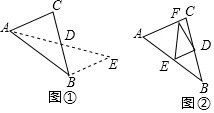 (1)阅读理解:
(1)阅读理解:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
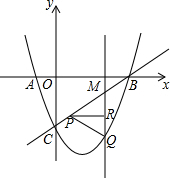 如图,抛物线y=ax2-(a+1)x-3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.
如图,抛物线y=ax2-(a+1)x-3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=32°,则下列结论错误的有( )
把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=32°,则下列结论错误的有( )| A. | ∠C′EF=32° | B. | ∠AEC=148° | C. | ∠BGE=64° | D. | ∠BFD=116° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com