
【题目】a,b分别是数轴上两个不同点A,B所表示的有理数,且|a|=5,|b|=2,A,B两点在数轴上的位置如图所示:
![]()
(1)试确定数a,b;
(2)A,B两点相距多少个单位长度?
(3)若C点在数轴上,C点到B点的距离是C点到A点距离的![]() ,求C点表示的数;
,求C点表示的数;
(4)点P从A点出发,先向左移动1个单位长度,再向右移动2个单位长度,再向左移动3个单位长度,再向右移动4个单位长度,依次操作2 019次后,求P点表示的数.
【答案】(1)a=-5,b=-2;(2)3;(3)![]() 或
或![]() ;(4)-1015.
;(4)-1015.
【解析】
(1)根据绝对值的定义结合由数轴得出a、b的符号即可得;
(2)根据数轴上两点间的距离公式即可得;
(3)设C点表示的数为x,分以下两种情况:点C在A、B之间、点C在点B右侧,利用两点间距离公式列方程求解.
(4)根据平移的性质可知,P点表示的数=-5-1+2-3+4-5+6+……-2017+2018-2019,计算结果即可.
解:(1)∵|a|=5,|b|=2,
∴a=5或-5,b=2或-2,
由数轴可知,a<b<0,
∴a=-5,b=-2;
(2)A、B两点间的距离是-2-(-5)=3;
(3)设C点表示的数为x,
∵C点到B点的距离是C点到A点距离的![]() ,
,
∴点C不可能在点A左侧.
下面分两种情况讨论:
当点C在A、B之间时,根据题意有:x-(-5)=3(-2 -x),
解得:![]() .
.
当点C在点B右侧时,根据题意有:x-(-5)=3[x-(-2)],
解得:![]()
∴C点表示的数为![]() 或
或![]() .
.
(4)P点表示的数=-5-1+2-3+4-5+6+……-2017+2018-2019
=-5+1009-2019
=-1015.


科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
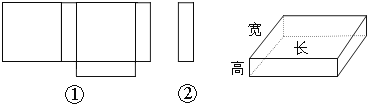
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
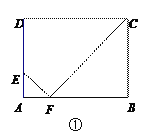
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)

(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
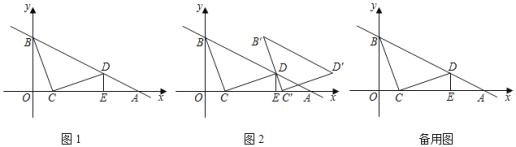
【题目】如图1,在平面直角坐标系中,直线y=-![]() x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
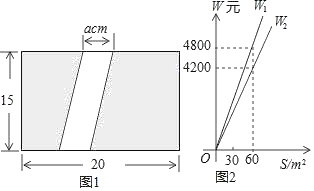
【题目】如图1,为美化校园环境,某校计划在一块长为20m,宽为15m的长方形空地上修建一条宽为a(m)的甬道,余下的部分铺设草坪建成绿地.
(1)甬道的面积为 m2,绿地的面积为 m2(用含a的代数式表示);
(2)已知某公园公司修建甬道,绿地的造价W1(元),W2(元)与修建面积S之间的函数关系如图2所示.①园林公司修建一平方米的甬道,绿地的造价分别为 元, 元.②直接写出修建甬道的造价W1(元),修建绿地的造价W2(元)与a(m)的关系式;③如果学校决定由该公司承建此项目,并要求修建的甬道宽度不少于2m且不超过5m,那么甬道宽为多少时,修建的甬道和绿地的总造价最低,最低总造价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)9﹣(﹣5)﹣(+2)+(﹣4)﹣5
(2)﹣|﹣7![]() |+(+3
|+(+3![]() )﹣5
)﹣5![]()
(3)![]() ﹣|﹣1
﹣|﹣1![]() |﹣(+2
|﹣(+2![]() )﹣(﹣2.75)
)﹣(﹣2.75)
(4)﹣9÷3+(![]() ﹣
﹣![]() )×12+(﹣3)2
)×12+(﹣3)2
(5)﹣5×(﹣3![]() )+(﹣9)×(3
)+(﹣9)×(3![]() )+17×(﹣3
)+17×(﹣3![]() )
)
(6)(![]() )÷(﹣
)÷(﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本拓展
旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
1.尝试探究:
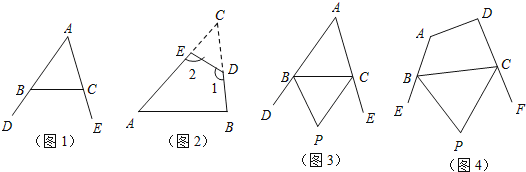
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
2.初步应用:
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2-∠C= ;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
3拓展提升:
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com