
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-分组法因式分解(带解析) 题型:解答题
阅读下列文字与例题将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.
例如:(1) am +an+ bm +bn=(am+bm)+(an+bn)
=m(a+b)+n(a+b)
=(a+b)(m+n)
(2)x2﹣y2﹣2y﹣1=x2﹣(y2+2y+1)
=x2﹣(y+1)2
=(x+y+1)(x﹣y﹣1)
试用上述方法分解因式a2+2ab+ac+bc+b2= .
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-分组法因式分解(解析版) 题型:解答题
阅读下列文字与例题将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.
例如:(1) am +an+ bm +bn=(am+bm)+(an+bn)
=m(a+b)+n(a+b)
=(a+b)(m+n)
(2)x2﹣y2﹣2y﹣1=x2﹣(y2+2y+1)
=x2﹣(y+1)2
=(x+y+1)(x﹣y﹣1)
试用上述方法分解因式a2+2ab+ac+bc+b2= .
查看答案和解析>>
科目:初中数学 来源:2012届浙江省衢州华茂八年级下学期第二次月考数学试卷 题型:填空题
阅读下列文字与例题
将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法。
例如:⑴am+an+bm+bn=(am+bm)+(an+bn)
=m(a+b)+n(a+b)
=(a+b)(m+n)
⑵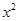 -
-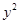 -
-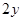 -
- =
=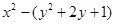
=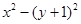
=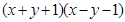
试用上述方法分解因式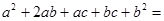 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com