
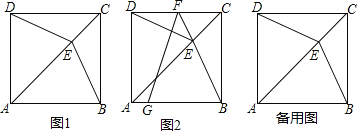
【题目】如图,在正方形ABCD中,点E为对角线AC上的一点,连接BE,DE.
(1)如图1,求证:△BCE≌△DCE;
(2)如图2,延长BE交直线CD于点F,G在直线AB上,且FG=FB.
①求证:DE⊥FG;
②已知正方形ABCD的边长为2,若点E在对角线AC上移动,当△BFG为等边三角形时,求线段DE的长。
【答案】(1)证明见解析;(2)①证明见解析;②DE=2(![]() ﹣1)
﹣1)
【解析】试题分析:(1)利用判定定理(SAS)可证;
(2)①利用(1)的结论与正方形的性质,只需证明∠FDE+∠DFG=90°即可;
②由DE⊥FG可构造直角三角形,利用等边三角形的性质及三角函数可求DE的长.
试题解析:(1)∵四边形ABCD是正方形,AC是其对角线,
∴∠DCE=∠BCE,CD=CB
在△BCE与△DCE中,

∴△BCE≌△DCE(SAS).
(2)①∵由(1)可知△BCE≌△DCE,
∴∠FDE=∠FBC
又∵四边形ABCD是正方形,
∴CD∥AB,
∴∠DFG=∠BGF,∠CFB=∠GBF,
又∵FG=FB,
∴∠FGB=∠FBG,
∴∠DFG=∠CFB,
又∵∠FCB=90°,
∴∠CFB+∠CBF=90°,
∴∠EDF+∠DFG=90°,
∴DE⊥FG
②如下图所示,
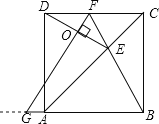
∵△BFG为等边三角形,
∴∠BFG=60°,
∵由(1)知∠DFG=∠CFB=60°,
在Rt△FCB中,∠FCB=90°,
∴FC=CBcot60°=![]() ,DF=2-
,DF=2-![]() ,
,
又∵DE⊥FG,
∴∠FDE=∠FED=30°,OD=OE,
在Rt△DFO中,
OD=DFcos30°=![]() -1,
-1,
∴DE=2(![]() -1)
-1)


科目:初中数学 来源: 题型:
【题目】在校园歌手大奖赛上,比赛规则为:七位评委打分,去掉一个最高分和一个最低分后,所剩数据取平均数即为选手的最后得分.七位评委给某位歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0,则这位歌手的最后得分是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,我市自2012年以来对家庭用电收费实行阶梯电价,即每月对每户居民的用电量分为三个档级收费,第一档为用电量在180千瓦时(含180千瓦时)以内的部分,执行基本价格;第二档为用电量在180千瓦时到450千瓦时(含450千瓦时)的部分,实行提高电价;第三档为用电量超出450千瓦时的部分,执行市场调节价格. 我市一位同学家今年2月份用电330千瓦时,电费为213元,3月份用电240千瓦时,电费为150元.已知我市的一位居民今年4、5月份的家庭用电量分别为160和 410千瓦时,请你依据该同学家的缴费情况,计算这位居民4、5月份的电费分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB//CD.理由如下: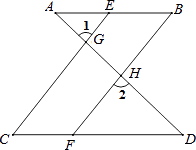
∵∠1=∠2 ,
且∠1=∠CGD ,
∴∠2=∠CG ,
∴CE//BF ,
∴∠=∠C两直线平行,同位角相等;
又∵∠B=∠C(已知),
∴∠BFD=∠B,
∴AB//CD .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车收费标准是:起步价8元,当路程超过2km时,每1km收费1.8元,如果某出租车行驶x(x>2km),则司机应收费(单位:元)( )
A. 8+1.8(x﹣2)B. 8+1.8xC. 8﹣1.8xD. 8﹣1.8(x﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com