
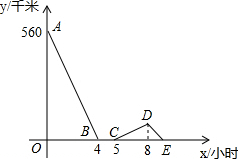
 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:分析 (1)根据题意得出慢车和快车经过4个小时后相遇,慢车行驶4小时的距离,快车3小时即可行驶完,进而求出快车速度以及利用两车速度之比得出慢车速度;
(2)根据图形即可得出B,D点表示的意义,进而求解;
(3)根据路程差=快车行驶的路程-慢车行驶的路程,进一步求出D点的坐标.
解答 解:(1)由题意可得出:慢车和快车经过4个小时后相遇,相遇后停留了1个小时,出发后两车之间的距离开始增大,快车到达甲地后两车之间的距离开始缩小,由图分析可知快车经过3个小时后到达甲地,此段路程慢车需要行驶4小时,因此慢车和快车的速度之比为3:4,
∴设慢车速度为3xkm/h,快车速度为4xkm/h,
∴(3x+4x)×4=560,
解得x=20,
∴慢车的速度,为60km/h,快车的速度为80km/h.
(2)由题意可得出:图中点B的实际意义是两车相遇,点D表示快车到达甲地;
(3)快车和慢车相遇地离甲地的距离为4×60=240km,
当慢车行驶了7小时后,快车已到达甲地,此时两车之间的距离为240-3×60=60km,
则D(8,60).
故答案为:(1)60,80;(2)两车相遇,快车到达甲地;(3)D(8,60).
点评 此题主要考查了一次函数的应用,根据题意得出B,D点表示的意义是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
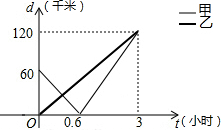 甲、乙两船沿直线航道AC匀速航行,甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行,设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,下列说法:①乙船的速度是40千米/时;②甲船航行1小时到达B处;③甲、乙两船航行0.6小时相遇;④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的个数是( )
甲、乙两船沿直线航道AC匀速航行,甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行,设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,下列说法:①乙船的速度是40千米/时;②甲船航行1小时到达B处;③甲、乙两船航行0.6小时相遇;④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )
如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{2}$ | C. | 2+2$\sqrt{3}$ | D. | 2+2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
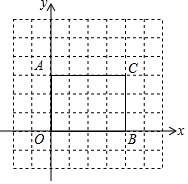 如图所示,矩形AOBC各点的坐标分别为A(0,3),O(0,0),B(4,0),C(4,3).以原点O为位似中心,将这个矩形缩小为原来的$\frac{1}{2}$,写出新矩形A′O′B′C′各顶点的坐标并画出图形(只要画出一个).
如图所示,矩形AOBC各点的坐标分别为A(0,3),O(0,0),B(4,0),C(4,3).以原点O为位似中心,将这个矩形缩小为原来的$\frac{1}{2}$,写出新矩形A′O′B′C′各顶点的坐标并画出图形(只要画出一个).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
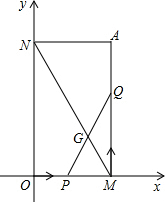 如图,已知过点A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.设PQ与MN交于点G.
如图,已知过点A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.设PQ与MN交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,不能推出四边形ABCD是矩形的是( )
如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,不能推出四边形ABCD是矩形的是( )| A. | BC=$\sqrt{3}$CD | B. | ∠A=90° | C. | AD=BC | D. | AB∥CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com