
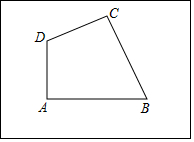
 小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案:
小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案:分析 (1)首先作出AD和AB的垂直平分线,两线的交点就是圆心O的位置,再以O为圆心,DO长为半径画圆即可;连接BD、CO,证明CO=DO即可;
(2)首先利用勾股定理计算出BD的长,进而可得⊙O的半径,再利用圆的面积公式进行计算即可.
解答 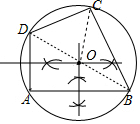 解:(1)小明说法正确,如图所示:
解:(1)小明说法正确,如图所示:
点C在⊙O上,
理由:连接BD、CO,
∵∠A=90°,
∴BD是⊙O的直径,
∵BO=DO,
∴点O是BD的中点,
∵∠DCB=90°,
∴CO=$\frac{1}{2}$BD,
∴CO=DO,
∴点C在⊙O上;
(2)∵AD=6米,AB=8米,
∴BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=10(米),
∴DO=5米,
∴小亮家圆形花坛的面积为25π米2.
故答案为:25π.
点评 此题主要考查了作图--应用设计与作图,以及圆周角定理,勾股定理的应用,关键是掌握半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1≤y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
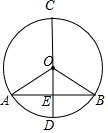 如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax2+bx+c=0 | B. | x2-y-1=0 | C. | $\frac{1}{x}$+x=1 | D. | x2=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
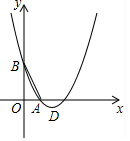 如图,已知抛物线y1=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.
如图,已知抛物线y1=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com