
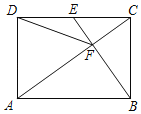
【题目】如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论正确的是_____.
①△ADC∽△CFB;②AD=DF;③![]() ;④
;④![]() =
=![]()
【答案】①②④.
【解析】
易得∠ADC=∠BCD=90°及∠CAD=∠BCF,从而可得△ADC∽△CFB;过点D作DM∥BE,交AC于N,交AB于M,可得DM垂直平分AF,则可得DF=DA;设CE=a,AD=b,则CD=2a由△ADC∽△CFB,可得![]() ,变形可判定③;根据E是CD边的中点,可得比例式,再结合△CEF∽△ABF,可判断④.
,变形可判定③;根据E是CD边的中点,可得比例式,再结合△CEF∽△ABF,可判断④.
解:∵BE⊥AC,∠ADC=∠BCD=90°
∴∠BCF+∠ACD=∠CAD+∠ACD
∴∠CAD=∠BCF
∴△ADC∽△CFB
∴①正确;
如图,过点D作DM∥BE,交AC于N,交AB于M
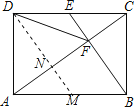
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形.
∴BM=DE=![]() DC.
DC.
∴BM=AM.
∴AN=NF.
∵BE⊥AC,DM∥BE,
∴DN⊥AF.
∴DM垂直平分AF.
∴DF=DA.
故②正确;
设CE=a,AD=b,则CD=2a,
由△ADC∽△CFB,可得![]() ,
,
∴b=![]() a.
a.
∴![]() ,
,
∴![]() .
.
故③错误;
∵E是CD边的中点
∴CE:AB=1:2
又∵CE∥AB
∴△CEF∽△ABF
∴![]() =
=![]() =
=![]() .
.
故④正确.
故答案为:①②④


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,∠ADC=90°,AD∥BC,点E在BC上,点F在AC上,∠DFC=∠AEB.
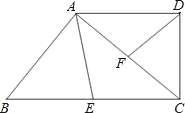
(1)求证:△ADF∽△CAE;
(2)当AD=8,DC=6,点E、F分别是BC、AC的中点时,求BC的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察猜想:
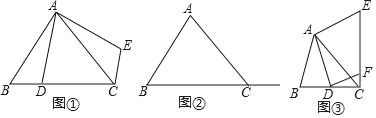
在Rt△ABC中,∠BAC=90°,AB=AC,点D在边BC上,连接AD,把△ABD绕点A逆时针旋转90°,点D落在点E处,如图①所示,则线段CE和线段BD的数量关系是 ,位置关系是 .
(2)探究证明:
在(1)的条件下,若点D在线段BC的延长线上,请判断(1)中结论是还成立吗?请在图②中画出图形,并证明你的判断.
(3)拓展延伸:
如图③,∠BAC≠90°,若AB≠AC,∠ACB=45°,AC=![]() ,其他条件不变,过点D作DF⊥AD交CE于点F,请直接写出线段CF长度的最大值.
,其他条件不变,过点D作DF⊥AD交CE于点F,请直接写出线段CF长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
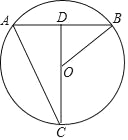
【题目】如图,点C在⊙O上,联结CO并延长交弦AB于点D, ![]() ,联结AC、OB,若CD=40,AC=20
,联结AC、OB,若CD=40,AC=20![]() .
.
(1)求弦AB的长;
(2)求sin∠ABO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
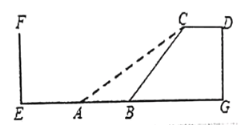
【题目】速滑运动受到许多年轻人的喜爱。如图,四边形![]() 是某速滑场馆建造的滑台,已知
是某速滑场馆建造的滑台,已知![]() ,滑台的高
,滑台的高![]() 为
为![]() 米,且坡面
米,且坡面![]() 的坡度为
的坡度为![]() .后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为
.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为![]() .
.
(1)求新坡面![]() 的坡角及
的坡角及![]() 的长;
的长;
(2)原坡面底部![]() 的正前方
的正前方![]() 米处
米处![]() 是护墙
是护墙![]() ,为保证安全,体育管理部门规定,坡面底部至少距护墙
,为保证安全,体育管理部门规定,坡面底部至少距护墙![]() 米。请问新的设计方案能否通过,试说明理由(参考数据:
米。请问新的设计方案能否通过,试说明理由(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).
(1)求抛物线的表达式,并写出其顶点坐标;
(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
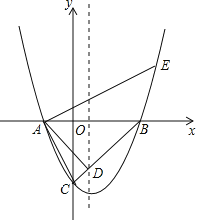
【题目】如图所示,在平面直角坐标系![]() 中,抛物线与
中,抛物线与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,
,![]() 与抛物线的对称轴相交于点
与抛物线的对称轴相交于点![]() .
.
(1)求该抛物线的表达式,并直接写出点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在射线
在射线![]() 上,若
上,若![]() 与
与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、B(4,0)两点,与y轴交于点C(0,3).

(1)求抛物线的解析式;
(2)在x轴下方的抛物线上是否存在一点P,使△PAB的面积等于△ABC的面积?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com