
分析 (1)分类讨论:2≤x≤8,8<x≤23,根据楼层的价格变化,可得函数解析式;
(2)分类讨论:2≤x≤8,8<x≤23,根据首付款与筹备款的不等式关系,可得答案.
解答 解:(1)每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式为
y=$\left\{\begin{array}{l}{20x+2840}&{(2≤x≤8)}\\{40x+2680}&{(8<x≤23)}\end{array}\right.$;
(2)由(1)得当2≤x≤8时,(20x+2840)×120×30%=36(20x+2840)=36(20×8+2840)=108000<120000,
则2楼到8楼的楼层可任意选;
当8<x≤23时,(40x+2680)××30%=36(40x+2680)≤120000,
x<$\frac{49}{3}$,x是正整数,
8<x≤16,9层到6层任意楼层都可以购买,
综上所述,用方案一购房,他可以任意购买2层到16楼层的商品房.
点评 本题考查的是用一次函数解决实际问题,读懂题目信息,找出数量关系表示出各楼层的单价以及是交房款的关系式是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图所示:
如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
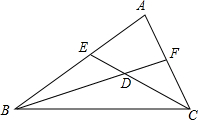 如图,在△ABC中,BF与CE交于点D,若BF和CE分别平分∠ABC和∠ACB.
如图,在△ABC中,BF与CE交于点D,若BF和CE分别平分∠ABC和∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 应当的 | B. | 不应当的 | C. | 没有影响 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com