练习册

  • 练习册
  • 试题
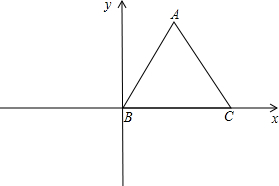
    精英家教网 > 初中数学 > 题目详情
    精英家教网如图所示，已知等边三角形ABC边长为2，写出点A、B、C的坐标，并画出以y轴为对称轴的等边三角形A1B1C1．
    分析：根据等边三角形ABC边长为2，可知B，C的坐标，再利用勾股定理求出三角形的高，就可求出A的坐标．从三角形的各顶点向y轴引垂线并延长相同长度，找到对应点顺次连接．
    解答：精英家教网解：从A点作高AD根据勾股定理可知BD=1，AD=
    		3
    ，
    所以A（1，
    		3
    ）、B（0，0）、C（2，0）．（2分）
    点评：本题综合考查了直角坐标系及轴对称图形的性质，作轴对称图形关键是找到图形的对应点．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知：如图所示，△ABC是等边三角形，D是AC中点，延长BC至E，使CE=CD，连接DE，
    ①试判断△DBE是什么三角形？并证明你的结论．
    ②若BC=2.2，求S△ABD（结果保留三个有效数字．提示：BD=
    		3
    2
    AB，
    		3
    =1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图所示，点C在线段AB上，分别以AC、BC为一边作为等边△ACM和等边△BCN，连接AN、BM．
    （1）求证：AN=BM；
    （2）设AN、BM相交于点D，求证：∠ADB=120°；
    （3）如果A、C、B三点不在同一直线上，那么AN=BM是否仍然成立？如果成立，加以证明；如果不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：新课程学习手册　数学　八年级(下) 配人教课标版 题型：044

    如图所示，已知：分别以△ABC的三边为边长，在BC边的同侧作三个等边三角形，即△ABD，△BCE，△ACF，请说明四边形ADEF是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

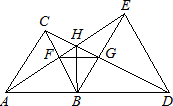    如图所示，已知△ABC和△BDE都是等边三角形，且A、B、D三点共线．下列结论：①AE=CD；②BF=BG；③HB平分∠AHD；④∠AHC=60°，⑤△BFG是等边三角形；⑥FG∥AD．其中正确的有


    1. A.
      3个
    2. B.
      4个
    3. C.
      5个
    4. D.
      6个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

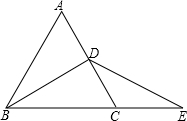    已知：如图所示，△ABC是等边三角形，D是AC中点，延长BC至E，使CE=CD，连接DE，
    ①试判断△DBE是什么三角形？并证明你的结论．
    ②若BC=2.2，求S△ABD（结果保留三个有效数字．提示：BD=数学公式AB，数学公式=1.732）

    查看答案和解析>>

    同步练习册答案