
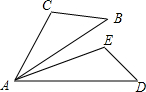
 如右图,已知∠EAD=30°,△ADE绕着点A旋转50°后能与△ABC重合,则∠BAE=________度.
如右图,已知∠EAD=30°,△ADE绕着点A旋转50°后能与△ABC重合,则∠BAE=________度.科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2014年中考数学二轮精品复习动点型问题练习卷(解析版) 题型:解答题
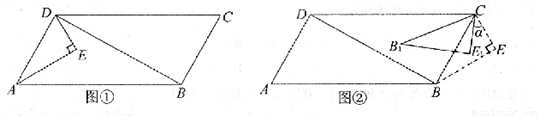
已知:如图①,在平行四边形ABCD中,AB=12,BC=6,AD⊥BD.以AD为斜边在平行四边形ABCD的内部作Rt△AED,∠EAD=30°,∠AED=90°.

(1)求△AED的周长;
(2)若△AED以每秒2个单位长度的速度沿DC向右平行移动,得到△A0E0D0,当A0D0与BC重合时停止移动,设运动时间为t秒,△A0E0D0与△BDC重叠的面积为S,请直接写出S与t之间的函数关系式,并写出t的取值范围;
(3)如图②,在(2)中,当△AED停止移动后得到△BEC,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点P、与直线CB交于点Q.是否存在这样的α,使△BPQ为等腰三角形?若存在,求出α的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(重庆A卷)数学(解析版) 题型:解答题
已知,如图①,在平行四边形ABCD中,AB=12,BC=6,AD⊥BD。以AD为斜边在平行四边形ABCD的内部作Rt△AED,∠EAD=300,∠AED=900。
(1)求△AED的周长;
(2)若△AED以每秒2个长度单位的速度沿DC向右平行移动,得到△A0E0D0,当A0D0与BC重合时停止移动。设移动时间为t秒,△A0E0D0与△BDC重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出t的取值范围;
(3)如图②,在(2)中,当△AED停止移动后得到△BEC,将△BEC绕点C按顺时针方向旋转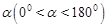 ,在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点P、与直线CB交于点Q。是否存在这样的
,在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点P、与直线CB交于点Q。是否存在这样的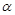 ,使△BPQ为等腰三角形?若存在,求出
,使△BPQ为等腰三角形?若存在,求出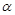 的度数;若不存在,请说明理由。
的度数;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com